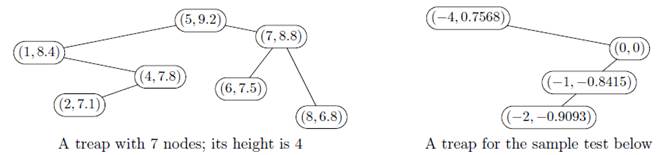
9519. Плохой Treap
Treap, известное как
декартово дерево, представляет собой структуру данных, которая хранит набор
ключей в бинарном дереве поиска.
Каждая вершина дерева
характеризуется парой (x, y).
x значения
вершин – значения сохраненных ключей. Они удовлетворяют правилу "поиска в бинарном
дереве": все x значения левого поддерева меньше значения x в
корне, а все x значения правого поддерева больше значения x в
корне.
y значения
вершин удовлетворяют правилу "кучи": y значение вершины
меньше или равно y значению родителя.
y значение
для каждого созданного узла обычно выбирается случайным образом в соответствии
с некоторым распределением. Это приводит к хорошей средней временной сложности
многих операций.
Поскольку эта структура
данных объединяет некоторые свойства двоичного дерева поиска и кучи, ее имя
является термином "portmanteau", состоящим из двух слов: TRee + hEAP = TREAP.
Бенджамин решил, что
недетерминизм в процедуре выбора значения y является плохим, поскольку в
этом случае время выполнения запросов различно. Он решил рассчитать y для
каждого узла детерминировано на основе его значения x. Он выбрал
правило y = sin(x). Бенджамин особенно рад, что различные целые
числа x всегда будут давать различные y.
Барбара понимает, что хотя
недетерминированное декартово дерево показывает худшую производительность,
когда предоставляется "плохая" случайная последовательность,
детерминированное декартово дерево показывает худшую производительность, когда
предоставляется "плохой" набор ключей. Она хочет объяснить это
Бенджамину, показав ему n целочисленных ключей, которые, будучи
сохраненными в его структуре данных, сформируют дерево высоты n –"наиболее
несбалансированную" возможную ситуацию.
Помогите Барбаре предоставить
n таких ключей. Все эти ключи должны
помещаться в 32 - битовый знаковый тип.
Вход. Одно целое число n (1 ≤ n ≤ 50000).
Выход. Выведите n строк содержащих различные
целочисленные ключи. Все ключи должны лежать в интервале между -231 и
231 – 1 включительно. Декартово дерево, построенное на ключах по
правилу y = sin(x), должно иметь высоту n.
|
Пример входа |
Пример выхода |
|
4 |
-2 0 -1 -4 |
РЕШЕНИЕ
декартово
дерево
Анализ алгоритма
В задаче следует построить
декартово дерево из n вершин
максимальной глубины. Это возможно, например, если мы найдем такую монотонную последовательность
целых чисел xi, что последовательность
соответствующих синусов sin(xi) будет также монотонной. Далее конструктивно мы построим такую последовательность x1, x2, ..., xn, что x1 < x2 < ... < xn и sin(x1) < sin(x2)
< ... < sin(xn). Здесь yi = sin(xi).
Построим декартово дерево по
парам (xi, sin(xi)). Оно будет иметь высоту
n.
Конструктивно построим требуемую последовательность.
Поскольку синус является периодической функцией с периодом 2π, то будем
искать ее в виде sin(k(2π + ɛ)), где k = 0, 1, 2, … . Найдем
такое натуральное число A, для которого существует целое k, что A = 2πk + ɛ для как можно меньшего значения ɛ. Например, если перебрать A от 1 до 1000, то наименьшее ɛ достигается при A = 710. В этом случае 710 ≈ 2π * 113 + 0.00006028.
Пусть A = 710. Рассмотрим последовательность
sin(A), sin(2A), sin(3A), …,
sin(nA)
Значения элементов этой последовательности равны
sin(2π * 113 + ɛ), sin(2*2π * 113 + 2*ɛ), sin(3*2π * 113 + 3*ɛ), …,
sin(n*2π * 113 + n*ɛ)
или с учетом
периодичности эти значения эквивалентны
sin(ɛ), sin(2*ɛ), sin(3*ɛ), …, sin(n*ɛ)
Функция sin(x) на промежутке x ∈ [0; π/2] возрастающая.
Для того чтобы ряд приведенных выше действительных чисел был мнонотонно возрастающим,
достаточно выполнения неравенства: n*ɛ ≤ π/2. Максимальное
значение n, для которого указанное неравенство
имеет место при ɛ
= 0.00006028, равно
π/2 / ɛ ≈ 26058
В условии задачу следует решить для n = 50000. Функция sin(x) возрастает на промежутке x ∈ [-π/2;
π/2]. Поэтому для построения ответа можно взять не только
положительные, но и отрицательные значения xi.
Реализация
алгоритма
Читаем входное значение
n.
scanf("%d", &n);
На отрезке [1..1000] находим такое натуральное А, для
которого при представлении в виде A = 2πk + ɛ значение
ɛ будет
наименьшим.
int bestStep = 0;
double bestMod = 2 * PI;
for (i = 1; i <
1000; i++)
{
double mod = fmod(i, 2.0 * PI);
if (mod < bestMod)
{
bestMod = mod;
bestStep = i;
}
}
Значение x = bestStep будет равно 710.
x = bestStep;
Выводим искомую последовательность из n элементов:
-n/2 * 710, (-n/2 + 1) *
710, (-n/2 + 2) * 710, …
i = -n / 2;
for (j = 0; j <
n; j++)
{
printf("%d\n", x*i);
i++;
}