9557. Ящики и
шары
В ряду стоят n ящиков. У Вас есть неограниченное количество шаров n разных цветов. Разместите по одному
шару в каждый ящик таким образом, чтобы в соседних ящиках не оказалось шаров
одного цвета. Сколько существует различных вариантов размещения шаров по
ящикам?
Вход. Одно
целое число n (1 ≤ n ≤ 109).
Выход. Выведите
количество различных вариантов размещения шаров по ящикам, вычисленное по
модулю 109 + 7.
|
Пример
входа |
Пример
выхода |
|
3 |
12 |
РЕШЕНИЕ
степень
Анализ алгоритма
В первый ящик можно положить
любой из n шаров. Цвет шара во втором ящике должен
отличаться от цвета шара в первом. Поэтому во второй ящик можно положить шар
любого из n – 1 оставшихся цветов. В i-ый ящик можно положить шар любого
цвета, отличного от цвета шара в (i –
1)-ом ящике.
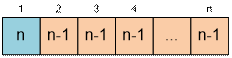
Таким образом, количество
различных вариантов размещения шаров по ящикам равно
n * (n
– 1)n – 1 mod 109 + 7
Реализация
алгоритма
Определим
модуль, по которому будут проводиться вычисления.
#define MOD
1000000007
Функция
powmod вычисляет значение xn mod m.
long long
powmod(long long x, long long n, long long m)
{
if (n ==
0) return 1;
if (n % 2
== 0) return powmod((x * x) % m, n / 2,
m);
return (x *
powmod(x, n - 1, m)) % m;
}
Основная часть программы. Читаем входное значение n.
scanf("%lld",
&n);
Вычисляем
и выводим ответ.
res = (powmod(n - 1, n - 1, MOD) *
n) % MOD;
printf("%d\n",
res);
Java реализация
import java.util.*;
public class Main
{
public final static long MOD = 1000000007;
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long res = (PowMod(n - 1, n - 1, MOD) * n) % MOD;
System.out.println(res);
con.close();
}
}
Python реализация – собственная
функция степени
Функция
myPow вычисляет
значение xn mod m.
def myPow(x, n, m):
if (n == 0): return 1
if (n % 2 == 0): return myPow((x
* x) % m, n / 2, m)
return (x *
myPow(x, n - 1, m)) % m
Основная часть программы. Определим
модуль mod = 109 + 7, по которому будем выполнять
вычисления.
mod = 10 ** 9 + 7
Читаем входное значение n.
n = int(input())
Вычисляем и выводим ответ.
print(n * myPow(n - 1, n - 1, mod)
% mod)
Python реализация
Определим
модуль mod = 109 +
7, по которому будем
выполнять вычисления.
mod = 10 ** 9 + 7
Читаем входное значение n.
n = int(input())
Вычисляем и выводим ответ.
print(n * pow(n - 1, n - 1, mod) % mod)