9557. Bins and balls
There are n boxes
arranged in a row. You have an unlimited supply of balls in n different
colors. Place one ball in each box in such a way that no two adjacent boxes
contain balls of the same color. How many different arrangements of balls in
the boxes are possible?
Input. One integer n (1 ≤ n ≤ 109).
Output. Print the number
of different arrangements of balls in the boxes, computed modulo 109 + 7.
|
Sample
input |
Sample
output |
|
3 |
12 |
SOLUTION
power
Algorithm analysis
In the first box, you can place any of the n balls. The color of the
ball in the second box must differ from the color of the ball in the first box.
Therefore, in the second box, you can place a ball of any of the remaining n
– 1 colors. In the i-th box, you can place a ball of any color that is
different from the color of the ball in the (i – 1)-th box.
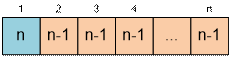
Thus, the number of different ways to arrange the balls in
the boxes is equal to
n * (n
– 1)n – 1 mod 109 + 7
Algorithm
implementation
Let’s
define the modulus MOD = 109 + 7 for the computations.
#define MOD
1000000007
The powmod
function computes the value of xn
mod m.
long long
powmod(long long x, long long n, long long m)
{
if (n ==
0) return 1;
if (n % 2
== 0) return powmod((x * x) % m, n / 2,
m);
return (x *
powmod(x, n - 1, m)) % m;
}
The main
part of the program. Read the input value of n.
scanf("%lld",
&n);
Compute and
print the answer.
res = (powmod(n - 1, n - 1, MOD) *
n) % MOD;
printf("%d\n",
res);
Java implementation
import java.util.*;
public class Main
{
public final static long MOD = 1000000007;
static long PowMod(long x, long n, long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);
return (x * PowMod(x, n - 1, m)) % m;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long res = (PowMod(n - 1, n -
1, MOD) * n) % MOD;
System.out.println(res);
con.close();
}
}
Python implementation – function myPow
The myPow
function computes the value of xn
mod m.
def myPow(x, n, m):
if (n == 0): return 1
if (n % 2 == 0): return myPow((x * x) % m, n / 2, m)
return (x * myPow(x, n - 1, m)) %
m
The main
part of the program.
Specify the modulus mod
= 109 + 7 to be used for the computations.
mod = 10 ** 9 + 7
Read the input value of n.
n = int(input())
Compute and print the answer.
print(n * myPow(n - 1, n - 1, mod)
% mod)
Python implementation
Let’s
define the modulus mod = 109 + 7 for the computations.
mod = 10 ** 9 + 7
Read the input value of n.
n = int(input())
Compute and print the answer.
print(n * pow(n - 1, n - 1, mod)
% mod)