9591. Лексикография
Люси любит
буквы. В школе она изучала понятие лексикографического порядка и теперь с
интересом играет с ним.
Сначала она
попробовала составить лексикографически наименьшее слово из заданного набора
букв – это оказалось
совсем просто! Затем она решила составить несколько слов и сделать так, чтобы
одно из них было минимальным в лексикографическом порядке. Это оказалось уже
значительно сложнее.
Формально Люси
хочет составить n слов длины l каждое из заданных n * l букв так, чтобы k-ое слово в
лексикографически отсортированном списке было лексикографически наименьшим из
возможных.
Вход. В первой строке заданы
три целых числа n, l и k (1 ≤ k ≤ n ≤ 1000, 1 ≤ l ≤ 1000) – количество слов, длина
каждого слова и индекс слова, которое Люси хочет минимизировать.
Во второй строке записана
строка из n * l строчных букв английского алфавита.
Выход. Выведите n слов по l букв в каждом, по одному
слову в строке, используя все буквы из входных данных. Слова должны быть
отсортированы в лексикографическом порядке, при этом k-ое слово должно быть
лексикографически как можно меньшим. Если существует несколько корректных
ответов с одинаковым минимальным k-ым словом, выведите любой из
них.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3
2 2 abcdef |
ad bc ef |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
2
3 1 abcabc |
aab bcc |
РЕШЕНИЕ
жадность
Анализ алгоритма
Лексикографический порядок слов определяется посимвольно слева направо.
Поэтому, чтобы минимизировать k-ое слово, нужно как можно раньше (в
первых позициях) поставить в него наименьшие возможные буквы, не нарушая
сортировку всех слов.
Это приводит к следующему жадному алгоритму:
1. Отсортируем все буквы входной
строки по возрастанию.
2. Будем строить двумерный массив
символов
v[1
.. n][1 .. l],
где каждая строка – отдельное
слово.
3. Заполняем массив по столбцам
слева направо, так как именно столбцы соответствуют позициям в словах и влияют
на лексикографический порядок.
Заполнение первого столбца
1. В первый столбец раздаём буквы
только строкам с номерами от 1 до k, используя k наименьших доступных букв.
2. Эти буквы размещаются сверху
вниз, чтобы сохранялся лексикографический порядок.
3. Строки с номерами k + 1, …, n на этом этапе не заполняются, поскольку они не влияют на минимальность k-го слова.
Таким образом, мы гарантируем, что первый символ k-го слова минимален.
Заполнение следующих столбцов
Для каждого столбца j =
2, 3, …, l:
1. Среди строк 1,
…, k находим минимальный индекс pt, такой что строки pt и k совпадают на всех предыдущих столбцах 1, …, j – 1.
2. Это множество строк [pt,
k] – все слова, которые на текущем
префиксе неотличимы от k-го и потому обязаны оставаться не больше него.
3. В столбце j раздаём наименьшие доступные буквы только строкам с номерами от pt до k, сверху вниз.
4. Повторяем процесс, пока все l символов k-го слова не будут зафиксированы.
Заполнение остальных клеток
После того как k-ое слово полностью построено:
·
Все оставшиеся буквы можно распределить произвольным образом, не нарушая
лексикографическую сортировку.
·
Например, можно последовательно заполнять массив по строкам сверху вниз и
слева направо оставшимися буквами в отсортированном порядке.
Корректность
·
В каждом столбце мы минимизируем текущий символ k-го слова.
·
Мы выдаём одинаковые или неубывающие буквы всем словам, которые совпадают с
ним по префиксу, поэтому порядок слов не нарушается.
·
После завершения k-го слова
дальнейшие действия не могут сделать его больше.
Следовательно, полученное k-ое слово
является лексикографически наименьшим.
Пример
Рассмотрим следующий тест
6 3 6
fgahhfgaaebdcbbebc
Здесь нужно составить 6 слов длины 3, используя все буквы, так чтобы 6-е
слово в лексикографически отсортированном списке было минимальным.
Отсортируем строку входных букв:
aaabbbbccdeeffgghh
Всего 18 = 6 ∙ 3 букв, что соответствует размеру таблицы 6 × 3.
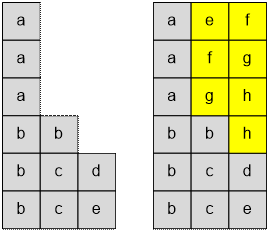
Столбец 1. Заполняем первый столбец буквами
сверху вниз от первой до шестой строки, так как именно она нас интересует.
Столбец 2. Теперь рассмотрим строки, чей
префикс совпадает с префиксом 6-й строки. Префикс 6-й строки после первого
столбца есть “b”. Совпадающими будут строки 4, 5 и
6. Минимальный номер такой строки pt =
4.
Во втором столбце раздаём минимальные доступные буквы строкам с номерами от 4 до 6.
Столбец 3. Снова ищем строки, чей префикс
совпадает с “bc” (после
заполненных двух столбцов). Совпадающими будут строки 5 и 6. Минимальный номер такой строки pt = 5. Раздаём минимальные доступные
буквы строкам с номерами от 5 до 6. Теперь 6-е слово полностью сформировано и
равно “bcd”.
Заполнение оставшихся букв
После фиксации 6-го слова
оставшиеся буквы можно распределить произвольным корректным образом. Например, заполним таблицу по строкам сверху вниз и слева направо
оставшимися буквами в лексикографическом порядке.
Рассмотрим первый тест
3 2 2
abcdef
Отсортируем входную строку букв:
abcdef
Нам следует заполнить матрицу из 3 слов по 2 буквы каждое, лексикографически
минимизировав при этом 2-е слово.

Сначала заполняем первый столбец буквами сверху вниз, только для строк с
1-й по 2-ю, поскольку именно они влияют на минимальность второго слова.
Далее переходим ко второму столбцу. Его следует заполнять, начиная с самой
ранней строки, префикс которой совпадает с префиксом 2-й строки. В данном
случае такой строкой является сама 2-я строка, поэтому pt = 2. Заполняем
второй столбец буквами от строки номер pt до 2-й строки.
После этого оставшиеся буквы распределяем в лексикографическом порядке по
строкам сверху вниз и слева направо, что завершает построение корректного
ответа.
Реализация алгоритма
cin >> n >> l >> k;
cin >> s;
Отсортируем
буквы входной строки. Текущей обрабатываемой буквой будет s[pos].
pos = 0;
sort(s.begin(), s.end());
Объявим матрицу результата
v, состоящую из n строк и l столбцов, где каждая строка
соответствует одному слову длины l.
vector<string> v(n, string(l, ' '));
Будем распределять буквы
по столбцу с номером j, заполняя строки с номерами от pt до k – 1 включительно
(нумерация строк начинается с нуля).
int pt = 0;
for (j = 0; j < l; j++)
{
for (i = pt; i <
k; i++)
v[i][j] = s[pos++];
Двигаем указатель pt вперед (pt++) до тех пор, пока j-ый символ (k – 1)-ой строки не совпадёт с j-ым символом строки номер pt. В результате pt указывает на строку с наименьшим
номером, которая на текущем шаге совпадает с префиксом строки k – 1.
while (v[pt][j] != v[k - 1][j]) pt++;
}
После этого заполняем
оставшиеся ячейки матрицы. Для этого последовательно проходим по строкам сверху
вниз и по столбцам слева направо, распределяя оставшиеся буквы.
for (i = 0; i < n; i++)
for (j = 0; j < l; j++)
if (v[i][j] == ' ') v[i][j] = s[pos++];
Выводим ответ.
for (i = 0; i < n; i++)
cout << v[i] << endl;