9597. Фотострельба
Фермер
Джон выстроил n своих коров,
пронумерованных 1 ... n, для
фотоснимка. Изначально ФД планировал, что i-ая
корова слева будет иметь номер ai,
и выписал перестановку a1,
a2, ..., an на листке бумаги. К
несчастью этот листок был похищен фермером Нхож.
Однако,
у ФД есть возможность восстановить перестановку, которую он изначально записал.
Перед тем, как листок с перестановкой был похищен, Бесси записала
последовательность b1, b2, ..., bn-1 такую,
что bi = ai + ai+1 для всех
i (1 ≤ i < n).
Основываясь
на информации от Бесси, помогите ФД восстановить “лексикографически
минимальную” перестановку a, которая может привести к
последовательности b. Перестановка x лексикографически меньше перестановки y, если для некоторого j,
xi = yi для всех i
< j и xj < yj (другими
словами, две перестановки идентичны до определённой точки, в которой x
меньше чем y). Гарантируется, что существует как минимум одна такая
перестановка a.
Вход. Первая строка содержит одно
целое число n (2 ≤ n ≤ 103). Вторая строка
содержит n – 1 целых
чисел b1, b2, ..., bn-1.
Выход. Выведите лексикографически
минимальную перестановку a1,
a2, ..., an.
|
Пример
входа |
Пример
выхода |
|
5 4 6 7 6 |
3 1 5 2 4 |
РЕШЕНИЕ
перебор
Анализ алгоритма
Число a1
может принимать значения от 1 до n.
При фиксированном значении a1
остальные числа последовательности a2,
..., an определяются
однозначно. Перебираем a1
от 1 до n, восстанавливаем
последовательность a и проверяем,
является ли она перестановкой чисел от 1 до n
(все ai должны
быть разные и находиться в промежутке от 1 до n). Как только восстановленная последовательность a
будет перестановкой, выводим ее и завершаем работу программы.
Поскольку
bi = ai + ai+1,
то ai+1 = bi – ai или ai
= bi-1 – ai-1.
Пример
Пусть a1 = 3. Тогда последовательность b = (4, 6, 7, 6) порождает следующую последовательность а:
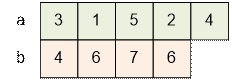
Последовательность
a = (3, 1, 5, 2, 4) является
перестановкой. Имеют место соотношения: 3 + 1 = 4, 1 + 5 = 6, 5 + 2 = 7 и 2 +
4 = 6.
Если, например, выбрать a1 = 1, то по входной
последовательности b = (4, 6, 7, 6) будет восстановлена следующая последовательность а:

Последовательность a = (1, 3, 3, 4, 2) не является перестановкой.
Реализация алгоритма
Объявим
рабочие массивы.
Массив used будет использоваться для проверки, является ли a
перестановкой.
#define MAX 1001
int a[MAX], b[MAX], used[MAX];
Читаем входные данные.
scanf("%d", &n);
for (i = 0; i < n - 1; i++)
scanf("%d", &b[i]);
Перебираем значение a0 от 1 до n.
for (a0 = 1; a0 <= n; a0++)
{
a[0] = a0;
Вычисляем элементы последовательности a по формуле ai = bi-1
– ai-1.
for (i = 1; i < n; i++)
a[i] = b[i - 1] - a[i - 1];
Обнуляем массив used.
for (i = 1; i <= n; i++)
used[i] = 0;
Проверяем,
является ли a перестановкой. Для этого каждое из значений ai должно встречаться в
последовательности только один раз, и находиться в промежутке от 1 до n. Переменная flag устанавливается
в 1, если последовательность a не является перестановкой.
flag = 0;
for (i = 0; i < n; i++)
{
if (a[i] < 1 || a[i] > n || used[a[i]])
{
flag = 1;
break;
}
used[a[i]] = 1;
}
Если последовательность a является
перестановкой, то выводим ее и завершаем работу программы.
if (flag == 0)
{
for (i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
return 0;
}
}
Python реализация
Читаем входные данные.
n = int(input())
b = list(map(int, input().split()))
Объявим
рабочие массивы.
Массив used будет использоваться для проверки, является ли a
перестановкой.
a = [0] * n
used = [0] * (n + 1)
Перебираем значение a0 от 1 до n.
for a0 in range(1, n + 1):
a[0] = a0
Вычисляем элементы последовательности a по формуле ai = bi-1
– ai-1.
for i in range(1, n):
a[i] = b[i - 1] - a[i - 1]
Обнуляем массив used.
for i in range(1, n + 1):
used[i] = 0
Проверяем,
является ли a перестановкой. Для этого каждое из значений ai должно встречаться в
последовательности только один раз, и находиться в промежутке от 1 до n. Переменная flag
устанавливается в 1, если последовательность a не является
перестановкой.
flag = 0
for i in range(n):
if a[i] < 1 or a[i] > n or used[a[i]]:
flag = 1
break
used[a[i]] = 1
Если последовательность a является
перестановкой, то выводим ее и завершаем работу программы.
if flag == 0:
print(*a)
break