9597. Photoshoot
Farmer John is arranging his n cows
numbered 1 ... n for a photoshoot.
Initially, FJ planned for the i-th cow from the left to be the cow
numbered ai, and wrote down the permutation a1, a2, ..., an
on a sheet of paper.
Unfortunately, that paper was recently stolen by Farmer Nhoj!
Fortunately, there might still be a chance for
FJ to recover the permutation that he originally wrote down. Before the sheet
was stolen, Bessie recorded the sequence b1, b2,
..., bn-1, which satisfies bi = ai + ai+1 for each i (1 ≤ i < n).
Based on Bessie’s information, help FJ
restore the “lexicographically minimum” permutation a, which could lead
to the sequence b. A permutation x is lexicographically smaller
than a permutation y if for some j, xi
= yi for all i < j and xj < yj (in other words, the two permutations are
identical up to a certain point, at which x is smaller than y).
It is guaranteed that at least one such a exists.
Input. The first line contains a single integer n (2 ≤ n ≤ 103). The second line contains n – 1 integers b1, b2, ..., bn-1.
Output. Print the lexicographically minimum permutation a1, a2, ..., an
.
|
Sample
input |
Sample
output |
|
5 4 6 7 6 |
3 1 5 2 4 |
SOLUTION
full search
Algorithm analysis
The number a1 can range from 1 to n.
Given a fixed value of a1,
the remaining numbers in the sequence a2, ..., an are uniquely
determined. Iterate a1
from 1 to n, restore the sequence a and verify whether it constitutes
a permutation of numbers from 1 to n (all ai must be distinct
and fall within the range from 1 to n). Once the reconstructed sequence a
forms a permutation, print it and terminate the program.
Since bi = ai + ai+1, then ai+1 = bi – ai or ai = bi-1
– ai-1.
Example
Let a1 = 3. Then sequence b = (4, 6, 7, 6) generates the following sequence à:
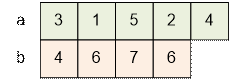
The sequence a = (3, 1, 5, 2, 4) is a permutation. The following
relationship holds: 3 + 1 = 4, 1 + 5 = 6, 5 + 2 = 7, and 2 +
4 = 6.
If, for
example, we choose a1 = 1, then the following
sequence à will be restored from the input sequence b = (4, 6, 7, 6):

The sequence a = (1, 3, 3, 4, 2) is not a
permutation.
Algorithm realization
Declare the
arrays. The array used will be used to verify whether a is a
permutation.
#define MAX 1001
int a[MAX], b[MAX], used[MAX];
Read the input data.
scanf("%d", &n);
for (i = 0; i < n - 1; i++)
scanf("%d", &b[i]);
Iterate over the value of a0 from 1 to n.
for (a0 = 1; a0 <= n; a0++)
{
a[0] = a0;
Compute the elements of the sequence a using the formula ai = bi-1 – ai-1.
for (i = 1; i < n; i++)
a[i] = b[i - 1] - a[i - 1];
Initialize the array used with zeroes.
for (i = 1; i <= n; i++)
used[i] = 0;
Check if a
is a permutation. Each value of ai must appear in
the sequence only once and be within the range from 1 to n. The variable
flag will be set to 1 if the sequence a is not a permutation.
flag = 0;
for (i = 0; i < n; i++)
{
if (a[i] < 1 || a[i]
> n || used[a[i]])
{
flag = 1;
break;
}
used[a[i]] = 1;
}
If the sequence a is a permutation, print it and terminate the
program.
if (flag == 0)
{
for (i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
return 0;
}
}
Python realization
Read the input data.
n = int(input())
b = list(map(int, input().split()))
Declare the lists. The list used
will be used to check if a is a permutation.
a = [0] * n
used = [0] * (n + 1)
Iterate over the value of a0 from 1 to n.
for a0 in range(1, n + 1):
a[0] = a0
Compute the elements of the sequence a using the formula ai = bi-1 – ai-1.
for i in range(1, n):
a[i] = b[i - 1] - a[i - 1]
Initialize the list used with zeroes.
for i in range(1, n + 1):
used[i] = 0
Check if a
is a permutation. Each value of ai must appear in the sequence only once and be within
the range from 1 to n. The variable flag will be set to 1 if the
sequence a is not a permutation.
flag = 0
for i in range(n):
if a[i] < 1 or a[i] > n or used[a[i]]:
flag = 1
break
used[a[i]] = 1
If the sequence a is a permutation, print it and terminate the
program.
if flag == 0:
print(*a)
break