9598. Гонки

Бесси участвует в гонке длиной k метров. Она начинает бежать со скоростью 0 метров в секунду. Каждую секунду она может увеличить свою скорость на 1 метр в секунду, оставить скорость неизменной или уменьшить скорость на 1 метр в секунду. Например, в первую секунду она может увеличить скорость на 1 метр в секунду и пробежать за эту секунду 1 метр, или оставить скорость 0 метров в секунду и пробежать 0 метров. Бесси не может сделать свою скорость меньше нуля.

Бесси всегда бежит к финишу и хочет финишировать после целого количества секунд. Кроме того, она не хочет прибежать слишком быстро, поэтому на финише её скорость не может превысить x метров в секунду. Бесси хочет узнать, как быстро она сможет закончить гонку для n различных величин x.

Вход. Первая строка содержит два целых числа k (1 ≤ k ≤ 10⁹) и n (1 ≤ n ≤ 1000). Каждая из следующих n строк содержит одно целое число x (1 ≤ x ≤ 10⁵).

Выход. Выведите n строк, каждая из них должна содержать одно целое число – минимальное количество времени, которое требуется Бесси, чтобы пробежать k метров и финишировать со скоростью меньшей либо равной x.

Пример.

При x = 1 оптимальное решение следующее:

· Увеличить скорость до 1 м/с, пробежать 1 м

· Увеличить скорость до 2 м/с, пробежать 2 метра, в сумме 3 метра

· Сохранить скорость 2 м/с, пробежать в сумме 5 метров

· Сохранить скорость 2 м/с, пробежать в сумме 7 метров

· Сохранить скорость 2 м/с, пробежать в сумме 9 метров

· Уменьшить скорость до 1 м/с пробежать в сумме 10 метров

При x = 3 оптимальное решение следующее:

· Увеличить скорость до 1 м/с, пробежать 1 м

· Увеличить скорость до 2 м/с, пробежать в сумме 3 метра

· Увеличить скорость до 3 м/с, пробежать в сумме 6 метров

· Сохранить скорость 3 м/с, пробежать в сумме 9 метров

· Сохранить скорость 3 м/с, после преодоления 10-го метра скорость 3 м/с

Приведём неверное решение при x = 3:

· Увеличить скорость до 1 м/с, пробежать 1 м

· Увеличить скорость до 2 м/с, пробежать в сумме 3 метра

· Увеличить скорость до 3 м/с, пробежать в сумме 6 метров

· Увеличить скорость до 4 м/с, пробежать в сумме 10 метров

Неверно, потому что скорость на финише Бесси равна 4.

Пример входа	Пример выхода
10 5 1 2 3 4 5	6 5 5 4 4

РЕШЕНИЕ

математика

Анализ алгоритма

Если бы у нас не было ограничения на скорость финиширования, Бесси было бы выгодно каждую секунду наращивать скорость на 1. То есть в первую секунду бежать 1 метр, во вторую секунду 2 метра и так далее. Однако при наличии ограничения выгодно до какого-то момента времени t₀ увеличивать скорость, а потом уменьшать, причем так чтобы на финише иметь скорость x. График зависимости скорости от времени имеет вид:

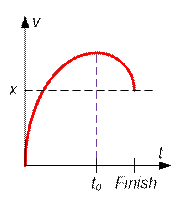
Пусть left – расстояние, которое Бесси пройдет до момента времени t₀ (разгон), right – расстояние от момента времени t₀ до времени финиширования (торможение).

Перебираем значение скорости Бесси: 1, 2, 3, … . Пока скорость меньше x, соответствующее пройденное расстояние добавляем в left. Когда скорость станет больше или равной x, расстояние будем прибавлять в left и right. Скорость перебираем до тех пор пока пройденное расстояние left + right не станет больше или равным длине маршрута k.

Реализация алгоритма

Функция solve возвращает минимальное количество времени, которое требуется Бесси, чтобы пробежать dist метров и финишировать со скоростью меньшей либо равной x.

int solve(int dist, int x)

{

Инициализируем расстояния left и right нулем. Время бега Бесси считаем в переменной t.

int left = 0, right = 0;

int t = 0;

Перебираем скорость: 1, 2, 3, … .

for (int speed = 1;; speed++)

{

left += speed;

t++;

За секунду номер t Бесси пробегает speed метров. Если Бесси суммарно пробежала расстояние, не меньшее dist, то возвращаем время t.

if (left + right >= dist) return t;

Если текущая скорость Бесси speed не меньше x, то за текущую секунду значение right следует увеличить на speed.

if (speed >= x)

{

right += speed;

t++;

Если Бесси суммарно пробежала расстояние, не меньшее dist, то возвращаем время t.

if (left + right >= dist) return t;

}

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &k, &n);

for (i = 0; i < n; i++)

{

Читаем значение скорости x. Выводим для нее ответ.

scanf("%d", &x);

printf("%d\n", solve(k, x));

}