9608. Taxi

Ivan and Sergey were invited to participate in a regional informatics olympiad.

Since they live in different towns, Ivan suggested taking a taxi to get to the olympiad venue.

The taxi departs from point A, where Ivan lives, heads to point B to pick up Sergey, and then continues to point C, where the olympiad takes place.

Given the distances between towns and the cost per kilometer of a taxi ride, determine how much more expensive the trip will be if the taxi picks up Sergey compared to going directly to the olympiad venue. It is assumed that the taxi always chooses the shortest available route.

Input. The first line contains five numbers: four integers and one real number:

· n – the number of towns,

· A – the number of the town where Ivan lives,

· B – the number of the town where Sergey lives,

· С – the number of the town where the olympiad takes place,

· d – the cost of traveling one kilometer by taxi.

The second line contains an integer m – the number of roads.

Then follow m lines, each describing one road: two integers representing the towns the road connects, and one real number – the length of the road in kilometers.

All town numbers are positive integers not exceeding 100.

Output. Print one real number – the extra cost of the trip if the taxi picks up Sergey, compared to going directly to the olympiad venue.

If there is no route from point A to point B or from point A to point C, print -1.

Sample input	Sample output
5 1 2 3 4.25 5 1 4 2.5 4 2 3 4 5 3 3 5 2 3 4 8	25.5

SOLUTION

graphs - Dijkstra

Algorithm analysis

In a weighted graph, Dijkstra's algorithm is used to determine:

· the shortest distance dist_ab from point A to point B;

· the shortest distance dist_ac from point A to point C;

· the shortest distance dist_bc from point B to point C;

Without picking up Sergey, Ivan travels a distance of dist_ac.

With a detour to pick up Sergey, the total distance becomes dist_ab + dist_bc.

The answer to the problem is:

(dist_ab + dist_bc – dist_ac) * d

This is the additional amount the trip costs due to picking up Sergey.

Example

The road graph is as follows:

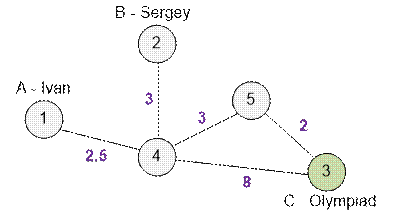
Let’s compute the shortest distances:

· the shortest path dist_ab from A to B is 5.5;

· the shortest path dist_ac from A to C is 7.5;

· the shortest path dist_bc from B to C is 8;

The distance Ivan travels without picking up Sergey: dist_ac = 7.5.

The distance with a detour to pick up Sergey: dist_ab + dist_bc = 5.5 + 8 = 13.5.

Thus, the answer to the problem is:

(dist_ab + dist_bc – dist_ac) * d = (5.5 + 8 – 7.5) * 4.25 = 6 * 4.25 = 25.5

Algorithm implementation

The graph is stored as a weighted adjacency matrix g. Declare an array of shortest distances dist and an array used, which holds information about the vertices for which the shortest distance is calculated.

#define MAX 110

double g[MAX][MAX], dist[MAX];

int used[MAX];

The Dijkstra function returns the length of the shortest path from vertex s to vertex f.

double Dijkstra(int s, int f)

{

memset(used, 0, sizeof(used));

for (i = 1; i <= n; i++) dist[i] = 1e18;

dist[s] = 0;

for (i = 1; i < n; i++)

{

double min = 1e18;

int w = -1;

for (j = 1; j <= n; j++)

if (used[j] == 0 && dist[j] < min) { min = dist[j]; w = j; }

if (min == 1e18) break;

for (j = 1; j <= n; j++)

if (used[j] == 0) dist[j] = minimum(dist[j], dist[w] + g[w][j]);

used[w] = 1;

}

return dist[f];

}

The main part of the program. Read the input data.

scanf("%d %d %d %d %lf", &n, &a, &b, &c, &d);

scanf("%d", &m);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++) g[i][j] = 1e18;

for (i = 0; i < m; i++)

{

scanf("%d %d %lf", &s, &f, &w);

g[s][f] = g[f][s] = w;

}

Compute the values of dist_ab, dist_bc, dist_ac.

double d1 = Dijkstra(a, b);

double d2 = Dijkstra(b, c);

double ds = Dijkstra(a, c);

If at least one of these values is equal to infinity, it means that the corresponding route does not exist – in this case print -1.

if (d1 == 1e18 || d2 == 1e18 || ds == 1e18) printf("-1\n");

Otherwise, print the result: (dist_ab + dist_bc – dist_ac) * d.

else printf("%lf\n", (d1 + d2 - ds) * d);