9616. Anti-palindromic strings
Two integers n and m are given. Find the number of strings of length n, which symbols belong to the alphabet
of size m, that do not contain
palindromes of length more than one as substrings.
Input.
First line contains the number of test cases t. Each test is a separate line with two integers n and m (1 ≤ n, m ≤ 109).
Output. For each test case print in
a separate line the required number of strings taken by modulo 109 + 7.
|
Sample input |
Sample output |
|
2 5 6 6 5 |
1920 1620 |
SOLUTION
exponentiation
Algorithm analysis
If a string does not contain a substring that is a palindrome of length 2
or length 3, then it does not contain a substring that is a palindrome of length greater than one.
If n = 1, then a string of length 1 can contain any of m letters. The required number of strings equals to m.
If m = 1 and n
> 1, the answer is 0, since there is only one string aa..aa and it contains the palindrome aa.
If n = 2, then the first position of the string can contain
any of m letters, and the second
position can contain any of m – 1 letters (the letters in the first and second
positions must not coincide, forming a palindrome). The number of strings equals to (m
* (m – 1)) mod 109 + 7.
Let the length of the input string be
greater than 2. Any of m letters can
be in the first position, and any of m
– 1 letters can be in the second position. The third position must be different
from the second (the second and third letters must not form a palindrome). The
third position must be different from the first (the first three letters must
not form a palindrome). This means that any of m – 2 letters can be in the third position.
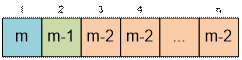
Following this logic, we conclude
that the letter at the i-th position must
differ from the letters at positions (i – 1) and (i – 2). The number of required string equals to (m * (m
– 1) * (m – 2)n – 2) mod 109 + 7.
Algorithm realization
Declare the module that will be
used for calculations.
#define MOD 1000000007
Function powmod finds the value of xn mod
m.
long long powmod(long long x, long long n, long long m)
{
if (n == 0) return 1;
if (n % 2 == 0) return powmod((x * x) % m, n / 2, m);
return (x * powmod(x, n - 1, m)) % m;
}
The main part of the
program. Read
the input data.
scanf("%d", &tests);
while (tests--)
{
scanf("%lld %lld", &n,
&m);
Calculate the answer depending on
the values of n and m.
if (n == 1) res = m; else
if (m == 1) res = 0; else // n > 1, m = 1: aa....a
if (n == 2) res = (m * (m - 1)) % MOD; else
res = ((m * (m - 1)) % MOD * powmod(m - 2,
n - 2, MOD)) % MOD;
Print the answer.
printf("%lld\n", res);
}