9628. Лягушка

Имеются n камней, пронумерованных от 1 до n. Для каждого i (1 ≤ i ≤ n) высота i-го камня равна h_i. Лягушка изначально находится на камне 1. Она повторяет следующее действие некоторое количество раз для достижения камня n: если лягушка находится на камне i, то она может прыгнуть или на камень i + 1 или на камень i + 2. Стоимость перемещения с i-го на j-ый камень равна | h_i − h_j |.

Найдите наименьшую стоимость перемещения лягушки на камень n.

Вход. Первая строка содержит количество камней n (2 ≤ n ≤ 10⁵). Вторая строка содержит целые числа h₁, h₂, ..., h_n (1 ≤ h_i ≤ 10⁴).

Выход. Выведите наименьшую стоимость перемещения лягушки на камень n.

Пример входа	Пример выхода
4 10 30 40 20	30

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть dp[i] содержит наименьшую стоимость перемещения лягушки на камень i. Тогда:

· dp[1] = 0 (перемещаться никуда не надо),

· dp[2] = | h₂ − h₁ |;

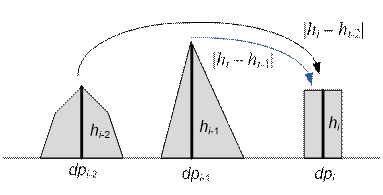
На i (i ≥ 3)-ый камень лягушка может прыгнуть:

· либо с (i – 1)-го камня со стоимостью |h_i – h_i-1|;

· либо с (i – 2)-го камня со стоимостью |h_i – h_i-2|;

Отсюда

dp[i] = min( dp[i – 1] + |h_i – h_i-1| , dp[i – 2] + |h_i – h_i-2| )

Пример

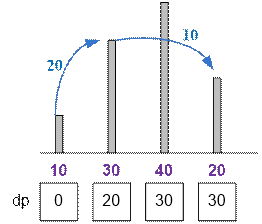
Для приведенного примера путь лягушки стоимостю 20 + 10 = 30 имеет вид:

· dp[1] = 0;

· dp[2] = | h₂ − h₁ | = | 30 − 10 | = 20;

· dp[3] = min( dp[2] + |h₃ – h₂| , dp[1] + |h₃ – h₁| ) =

min( 20 + | 40 − 30 | , 0 + | 40 − 10 | ) = min(30, 30) = 30;

· dp[4] = min( dp[3] + |h₄ – h₃| , dp[2] + |h₄ – h₂| ) =

min( 30 + | 20 − 40 | , 20 + | 20 − 30 | ) = min(50, 30) = 30;

Упражнение

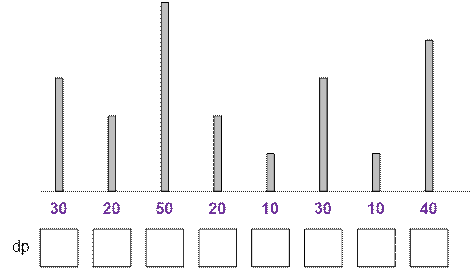
Заполните массив dp для следующего примера:

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 100001

int h[MAX], dp[MAX];

Читаем входные данные. Высоты камней заносим в массив h.

scanf("%d", &n);

for (i = 1; i <= n; i++)

scanf("%d", &h[i]);

Инициализируем dp[1] и dp[2].

dp[1] = 0;

dp[2] = abs(h[2] - h[1]);

Вычисляем значения dp[i] (3 ≤ i ≤ n).

for (i = 3; i <= n; i++)

{

a = dp[i - 1] + abs(h[i] - h[i - 1]);

b = dp[i - 2] + abs(h[i] - h[i - 2]);

dp[i] = min(a, b);

}

Выводим ответ.

printf("%d\n", dp[n]);

Java реализация

import java.util.*;

class Main

{

static int h[], dp[];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

h = new int[n+1];

dp = new int[n+1];

for(int i = 1; i <= n; i++)

h[i] = con.nextInt();

dp[1] = 0; dp[2] = Math.abs(h[2] - h[1]);

for (int i = 3; i <= n; i++)

{

int a = dp[i - 1] + Math.abs(h[i] - h[i - 1]);

int b = dp[i - 2] + Math.abs(h[i] - h[i - 2]);

dp[i] = Math.min(a, b);

}

System.out.println(dp[n]);

con.close();

}

}

Python реализация

Читаем входные данные. Высоты камней заносим в список h.

n = int(input())

h = list(map(int, input().split()))

Инициализируем список dp и присваиваем значения dp[1] и dp[2].

dp = [0] * (n + 1)

dp[1] = 0

dp[2] = abs(h[1] - h[0])

Вычисляем значения dp[i] (3 ≤ i ≤ n).

for i in range(3, n + 1):

a = dp[i - 1] + abs(h[i - 1] - h[i - 2])

b = dp[i - 2] + abs(h[i - 1] - h[i - 3])

dp[i] = min(a, b)

Выводим ответ.

print(dp[n])