9628. Frog

There are n stones, numbered from 1 to n. For each i (1 ≤ i ≤ n), the height of the i-th stone is h_i. The frog initially sits on stone 1. It repeats the following action several times to reach stone n: if the frog is on stone i, it can jump either to stone i + 1 or to stone i + 2. The cost of moving from the i-th to the j-th stone is |h_i − h_j |.

Find the minimum cost of moving the frog to stone n.

Input. The first line contains the number of stones n (2 ≤ n ≤ 10⁵). The second line contains integers h₁, h₂, ..., h_n (1 ≤ h_i ≤ 10⁴).

Output. Print the minimum cost of moving the frog to stone n.

Sample input	Sample output
4 10 30 40 20	30

SOLUTION

dynamic programming

Algorithm analysis

Let dp[i] be the minimum cost of moving the frog to stone i. Then:

· dp[1] = 0 (no need to move anywhere),

· dp[2] = | h₂ − h₁ |;

The frog can jump to the i (i ≥ 3)-th stone:

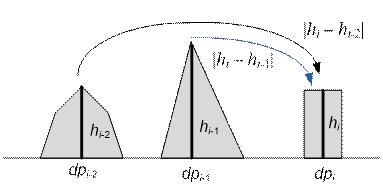
· either from the (i – 1)-th stone with a cost of |h_i – h_i-1|;

· or from the (i – 2)-th stone with a cost of |h_i – h_i-2|;

Hence

dp[i] = min( dp[i – 1] + |h_i – h_i-1| , dp[i – 2] + |h_i – h_i-2| )

Example

For the given example, the frog’s path with a cost of 20 + 10 = 30 looks like:

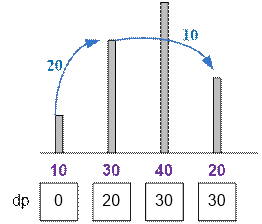
· dp[1] = 0;

· dp[2] = | h₂ − h₁ | = | 30 − 10 | = 20;

· dp[3] = min( dp[2] + |h₃ – h₂| , dp[1] + |h₃ – h₁| ) =

min( 20 + | 40 − 30 | , 0 + | 40 − 10 | ) = min(30, 30) = 30;

· dp[4] = min( dp[3] + |h₄ – h₃| , dp[2] + |h₄ – h₂| ) =

min( 30 + | 20 − 40 | , 20 + | 20 − 30 | ) = min(50, 30) = 30;

Exercise

Fill the dp array for the following example:

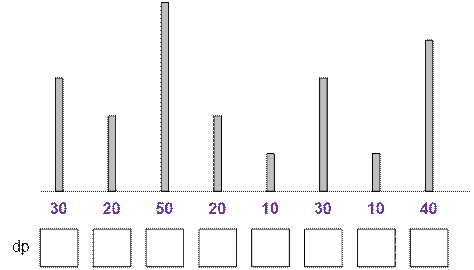
Algorithm realization

Declare the arrays.

#define MAX 100001

int h[MAX], dp[MAX];

Read the input data. Store the heights of the stones in the array h.

scanf("%d", &n);

for (i = 1; i <= n; i++)

scanf("%d", &h[i]);

Initialize the values of dp[1] and dp[2].

dp[1] = 0;

dp[2] = abs(h[2] - h[1]);

Compute the values of dp[i] (3 ≤ i ≤ n).

for (i = 3; i <= n; i++)

{

a = dp[i - 1] + abs(h[i] - h[i - 1]);

b = dp[i - 2] + abs(h[i] - h[i - 2]);

dp[i] = min(a, b);

}

Print the answer.

printf("%d\n", dp[n]);

Java realization

import java.util.*;

class Main

{

static int h[], dp[];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

h = new int[n+1];

dp = new int[n+1];

for(int i = 1; i <= n; i++)

h[i] = con.nextInt();

dp[1] = 0; dp[2] = Math.abs(h[2] - h[1]);

for (int i = 3; i <= n; i++)

{

int a = dp[i - 1] + Math.abs(h[i] - h[i - 1]);

int b = dp[i - 2] + Math.abs(h[i] - h[i - 2]);

dp[i] = Math.min(a, b);

}

System.out.println(dp[n]);

con.close();

}

}

Python realization

Read the input data. Store the heights of the stones in the list h.

n = int(input())

h = list(map(int, input().split()))

Initialize the list dp and assign values to dp[1] and dp[2].

dp = [0] * (n + 1)

dp[1] = 0

dp[2] = abs(h[1] - h[0])

Compute the values of dp[i] (3 ≤ i ≤ n).

for i in range(3, n + 1):

a = dp[i - 1] + abs(h[i - 1] - h[i - 2])

b = dp[i - 2] + abs(h[i - 1] - h[i - 3])

dp[i] = min(a, b)

Print the answer.

print(dp[n])