9632. The best team
Today, n programmers
have gathered. Each programmer has a rating that reflects his strength. The
rating is an integer between 0 and 109. Your rating as a
programmer is m. From all the programmers gathered today, you want
to choose two for your team. They must be selected in such a way that their
total rating is maximized but does not exceed your rating, as you want to be
the leader of this team.
Input. The first
line contains two integers: n (2 ≤ n ≤ 105)
– the number of programmers, and m (0 ≤ m ≤ 109)
– your rating. The second line contains n integers r1, r2,
..., rn (0 ≤ ri ≤ 109)
– the ratings of the programmers.
Output. Print a
single integer – the maximum sum of the ratings of the selected programmers, or
-1 if it is impossible to find such two people.
|
Sample
input 1 |
Sample
output 1 |
|
5 8 5 3 4 6 5 |
8 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
7 19 8 4 25 1 20 5 12 |
17 |
|
|
|
|
Sample
input 3 |
Sample
output 3 |
|
4 76 38 41 39 40 |
-1 |
SOLUTION
two pointers
Algorithm analysis
Sort the programmers’ ratings in the array v. To find
two programmers with the maximum total rating, we’ll use the two-pointer
technique.
Initialize the pointer low = 0 at the beginning of the array and the
pointer high = n – 1 at the
end of the array.
Among all possible sums v[low] + v[high],
not
exceeding m, find the maximum. If
v[low] + v[high] ≤ m, move the low pointer
forward. Otherwise, move the high pointer
backward. Continue this process until the pointers meet.
Example
Let’s consider the second test. Sort the
numbers and initialize the pointers. Simulate the algorithm’s execution. In
this case, m = 19: we are looking for two numbers with the
maximum sum that does not exceed 19.
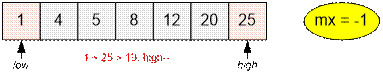



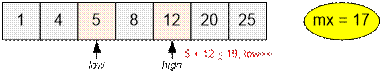
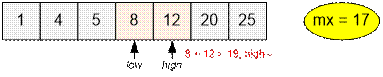
Algorithm realization
Read the input data.
scanf("%d %d", &n, &m);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);
Sort the programmers’ ratings.
sort(v.begin(),
v.end());
Initialize the pointers. The variable mx stores the
maximum sum of two elements.
int mx = -1, low = 0, high = n - 1;
The pointer low is moved forward, and the pointer high
is moved backward.
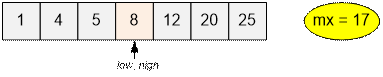
while (low < high)
{
Among all possible sums v[low] + v[high] that
do not exceed m find the maximum. If v[low] + v[high]
≤ m, move low
forward. Otherwise, move high backward.
if (v[low] + v[high] <= m)
{
mx = max(mx, v[low] + v[high]);
low++;
}
else high--;
}
Print the answer.
printf("%d\n", mx);