9635. Транспортная
система
Транспортная
система города Баку состоит из n перекрёстков и m двухсторонних
дорог, соединяющих их. Каждая дорога соединяет ровно два перекрёстка, причём
между любой парой перекрёстков может быть не более одной дороги. Более того, по
имеющимся дорогам можно добраться с любого перекрёстка до любого другого.
Расстоянием
между двумя перекрёстками называется минимальное количество дорог среди всех
возможных путей, соединяющих их.
Городской
мэр решил улучшить транспортную систему и поручил директору транспортного
управления построить новую дорогу. Однако мэр недавно купил новую машину и
ежедневно наслаждается поездками из дома на работу и обратно. Он не хочет,
чтобы расстояние между перекрёстком s, где находится его дом, и
перекрёстком t, где расположена его работа, уменьшилось после
строительства новой дороги.
Помогите
директору транспортного управления определить, сколько существует таких пар
несоединённых перекрёстков, что если между ними построить дорогу, расстояние
между s и t не уменьшится.
Вход. В первой строке заданы четыре
целых числа:
·
n (1 ≤ n ≤ 103) – количество
перекрёстков,
·
m (1 ≤ m ≤ 105) – количество
дорог,
·
s – перекрёсток, где находится
дом мэра,
·
t (1 ≤ s, t
≤ n, s ≠ t) –
перекрёсток, где находится работа мэра.
В
следующих m строках содержатся по два целых числа ui и vi
(1 ≤ ui, vi ≤ n, ui
≠ vi), означающие,
что между перекрёстками ui
и vi имеется двухсторонняя
дорога.
Выход. Выведите
количество пар несоединённых перекрёстков, добавление дороги между которыми не
уменьшит расстояние между перекрёстками s и t.
|
Пример
входа 1 |
Пример
выхода 1 |
|
5 4 1 5 1 2 2 3 3 4 4 5 |
0 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 4 3 5 1 2 2 3 3 4 4 5 |
5 |
РЕШЕНИЕ
графы,
поиск в ширину
Анализ алгоритма
Запустим поиск в
ширину из стартовой вершины s и финальной вершины f. Кратчайшие расстояния от s сохраним в массиве
distS, а от f – в массиве distF.
Обозначим через optDistance кратчайшее расстояние между s
и f в исходном графе.
Рассмотрим возможность
проведения новой дороги между вершинами i и j.
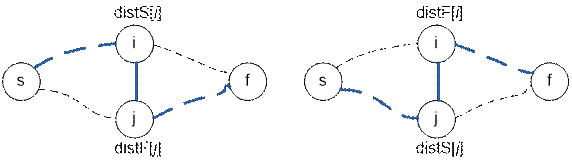
При добавлении дороги (i, j) в граф появляются новые
пути:
s → i → j → f длины distS[i] + 1 +
distF[j],
s → j → i → f длины distS[j] + 1 +
distF[i]
Если хотя бы
одно из этих расстояний окажется меньше optDistance, то добавление дороги (i, j) уменьшит
кратчайшее расстояние между s и f, а значит, она нам не подходит.
Остается
перебрать все возможные пары (i, j) и проверить, не приведёт ли новая дорога к уменьшению кратчайшего
расстояния между s и f.
Пример
Граф из
первого теста приведен слева. Кратчайшее расстояние от вершины 1 до вершины 5
равно 4. Какую бы новую дорогу мы ни добавили, это расстояние уменьшится.
Поэтому ни одной из требуемых дорог не существует.
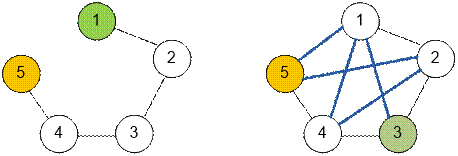
Граф из
второго теста показан справа. Кратчайшее расстояние от вершины 3 до вершины 5
равно 2. Жирными линиями обозначены возможные новые дороги. Независимо от того,
какую из этих дорог мы построим, расстояние между 3 и 5 не уменьшится.
Реализация алгоритма
Объявим константу MAX –
максимально возможное количество вершин графа.
#define MAX 1001
Объявим матрицу смежности g и
массивы кратчайших расстояний.
int g[MAX][MAX], distS[MAX], distF[MAX];
Функция bfs выполняет поиск в ширину из
вершины start. Ей передается массив dist,
в котором будут сохранены кратчайшие расстояния.
void bfs(int start, int *dist)
{
Инициализируем массив кратчайших расстояний dist.
for (int i = 0; i <= n; i++) dist[i] = -1;
dist[start] = 0;
Объявим очередь q и
добавим в нее стартовую вершину start.
queue<int> q;
q.push(start);
Пока очередь не пуста, извлекаем из нее вершину v.
while (!q.empty())
{
int v = q.front(); q.pop();
Перебираем все вершины to,
смежные с v. Если
вершина to еще не
посещена, вычисляем кратчайшее расстояние dist[to] и добавляем ее в очередь.
for (int to = 1; to <= n; to++)
if (g[v][to] && dist[to] == -1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d %d", &n, &m,
&s, &f);
memset(g, 0, sizeof(g));
Читаем неориентированный граф.
for (i = 0; i < m; i++)
{
scanf("%d
%d", &a, &b);
g[a][b] =
g[b][a] = 1;
}
Запускаем поиск в ширину из вершин s и f.
Кратчайшие расстояния сохраняем в массивах distS
и distF соответственно.
bfs(s, distS);
bfs(f, distF);
Кратчайшее расстояние между
s и f в исходном графе обозначим как optDistance.
optDistance = distS[f];
Перебирвем все пары вершин i и j и рассматриваем возможность
проведения между ними новой дороги. В переменной res подсчитываем
количество таких допустимых дорог.
res = 0;
for (i = 1; i <= n; i++)
for (j = i + 1; j <= n; j++)
Если между вершинами i и j ещё нет дороги, вычисляем длины
кратчайших путей: s → i → j → f и s → j → i → f. Если оба эти расстояния не меньше optDistance, то проведение такой дороги допустимо.
if (g[i][j] == 0)
{
if ((distS[i] + distF[j]
+ 1 >= optDistance) &&
(distS[j] + distF[i] + 1 >=
optDistance))
res++;
}
Выводим ответ.
printf("%d\n",
res);
Java реализация
import java.util.*;
public class Main
{
static int g[][], distS[], distF[];
static int n, m, s, f;
static void bfs(int start, int dist[])
{
Arrays.fill(dist,-1);
dist[start] = 0;
Queue<Integer> q = new LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for (int to = 1; to <= n; to++)
if (g[v][to] == 1 && dist[to] == -1)
{
q.add(to);
dist[to] = dist[v] + 1;
}
}
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
s = con.nextInt();
f = con.nextInt();
g = new int[n+1][n+1];
distS = new int[n+1];
distF = new int[n+1];
for (int i = 1; i <= m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
bfs(s, distS);
bfs(f, distF);
int optDistance = distS[f];
int res = 0;
for(int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
if (g[i][j] == 0)
{
if ((distS[i] + distF[j] + 1 >= optDistance) &&
(distS[j] + distF[i] + 1 >= optDistance))
res++;
}
System.out.println(res);
con.close();
}
}