9635. Transport system
The
transportation system of Baku consists of n intersections and m
bidirectional roads connecting them. Each road connects exactly two
intersections, and there can be at most one road between any pair of
intersections. Moreover, it is possible to travel between any two intersections
using the existing roads.
The distance
between two intersections is defined as the minimum number of roads among all
possible paths connecting them.
The city mayor
has decided to improve the transportation system and has instructed the
director of the transportation department to build a new road. However, the
mayor recently bought a new car and enjoys driving from home to work and back
every day. He does not want the distance between intersection s, where
his home is located, and intersection t, where his workplace is located,
to decrease after the new road is built.
Help the director
of the transportation department determine how many pairs of unconnected
intersections exist such that if a road is built between them, the distance
between s and t will not decrease.
Input. The first line contains four integers:
·
n (1 ≤ n ≤ 103) – the number
of intersections,
·
m (1 ≤ m ≤ 105) – the number
of roads,
·
s – the intersection where the mayor’s home is
located,
·
t (1 ≤ s,
t ≤ n, s ≠ t) – the intersection where the mayor’s
workplace is located.
The next m
lines each contain two integers ui
and vi (1 ≤ ui, vi ≤ n, ui ≠ vi), indicating that there is
a bidirectional road between intersections ui
and vi.
Output. Print the number of pairs of unconnected
intersections such that adding a road between them will not decrease the
distance between intersections s and t.
|
Sample
input 1 |
Sample
output 1 |
|
5 4 1 5 1 2 2 3 3 4 4 5 |
0 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
5 4 3 5 1 2 2 3 3 4 4 5 |
5 |
SOLUTION
graphs, breadth first
search
Algorithm analysis
Let’s run a breadth-first
search starting from the source vertex s and the destination vertex f.
Store the shortest distances from s in the array distS and from f
in the array distF.
Let optDistance
denote the shortest distance between s and f in the original
graph.
Now, let’s consider the
possibility of building a new road between vertices i and j.
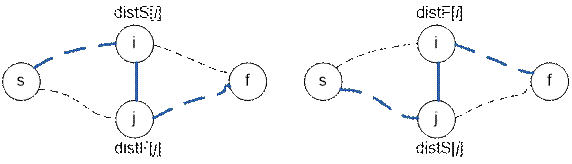
When adding a road (i,
j) to the graph, new paths are created:
s → i → j → f with length distS[i] + 1 + distF[j],
s → j → i → f with length distS[j] + 1 + distF[i]
If at least one
of these distances is smaller than optDistance, then adding the road (i, j) will decrease
the shortest distance between s and f, and thus it is not
suitable.
We now need to
check all possible pairs (i, j) and verify if adding a new road will
decrease the shortest distance between s and f.
Example
The graph from
the first test is shown on the left. The shortest distance from vertex 1 to
vertex 5 is 4. No matter which new road we add, this distance will decrease.
Therefore, none of the required roads exist.
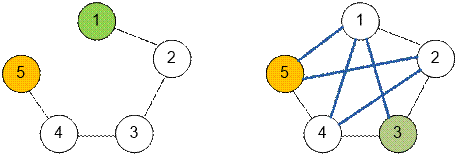
The graph from
the second test is shown on the right. The shortest distance from vertex 3 to
vertex 5 is 2. The possible new roads are marked with bold lines. Regardless of
which of these roads we build, the distance between 3 and 5 will not decrease.
Algorithm implementation
Define the constant MAX – the maximum possible number of vertices in
the graph.
#define MAX 1001
Declare the adjacency matrix g and the arrays for the shortest
distances.
int g[MAX][MAX], distS[MAX], distF[MAX];
The function bfs performs a breadth-first search
from the vertex start. It takes the array dist as input, where
the shortest distances will be stored.
void bfs(int start, int *dist)
{
Initialize the array of shortest distances dist.
for (int i = 0; i <= n; i++) dist[i] = -1;
dist[start] = 0;
Declare a queue q and add the starting vertex start to
it.
queue<int>
q;
q.push(start);
While the queue is not empty, dequeue the vertex v.
while (!q.empty())
{
int v = q.front(); q.pop();
Iterate through all vertices to adjacent to v.
If vertex to is not visited yet, compute the shortest distance dist[to] and add it to the queue.
for (int to = 1; to <= n; to++)
if (g[v][to] && dist[to] == -1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
}
The main part of the program. Read the input data.
scanf("%d %d %d %d", &n, &m,
&s, &f);
memset(g, 0, sizeof(g));
Read the undirected graph.
for (i = 0; i < m; i++)
{
scanf("%d
%d", &a, &b);
g[a][b] =
g[b][a] = 1;
}
Run a breadth-first search from vertices s and f. The
shortest distances are stored in the arrays distS and distF, respectively.
bfs(s, distS);
bfs(f, distF);
Let optDistance denote the shortest distance between s and f
in the original graph.
optDistance = distS[f];
Iterate through all pairs of vertices i and j and consider
the possibility of building a new road between them. The variable res
keeps track of the number of such valid roads.
res = 0;
for (i = 1; i <= n; i++)
for (j = i + 1; j <= n; j++)
If there is no road between vertices i and j, compute the lengths of the
shortest paths: s → i → j → f and s → j → i → f. If both of these distances are not less than optDistance,
then building such a road is allowed.
if (g[i][j] == 0)
{
if ((distS[i] + distF[j]
+ 1 >= optDistance) &&
(distS[j] + distF[i] + 1 >=
optDistance))
res++;
}
Print the answer.
printf("%d\n",
res);
Java implementation
import java.util.*;
public class Main
{
static int g[][], distS[], distF[];
static int n, m, s, f;
static void bfs(int start, int dist[])
{
Arrays.fill(dist,-1);
dist[start] = 0;
Queue<Integer> q = new LinkedList<Integer>();
q.add(start);
while(!q.isEmpty())
{
int v = q.poll();
for (int to = 1; to <= n; to++)
if (g[v][to] == 1 && dist[to] == -1)
{
q.add(to);
dist[to] = dist[v] + 1;
}
}
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
s = con.nextInt();
f = con.nextInt();
g = new int[n+1][n+1];
distS = new int[n+1];
distF = new int[n+1];
for (int i = 1; i <= m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
bfs(s, distS);
bfs(f, distF);
int optDistance = distS[f];
int res = 0;
for(int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++)
if (g[i][j] == 0)
{
if ((distS[i] + distF[j] + 1 >= optDistance) &&
(distS[j] + distF[i] + 1 >= optDistance))
res++;
}
System.out.println(res);
con.close();
}
}