9637. Dino and snow buildings
Dino travels to
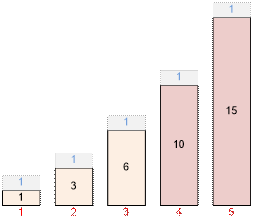
China (the Coronavirus was not yet spread there) and sees 109 buildings
there. The height of the first building is 1, the second building has the
height 1 + 2, the third one
is 1 + 2 + 3, etc. The height of the last building
is 1 + 2 + 3 + ... + 109 (all
heights are given in meters).
After a day, Dino
fell asleep and saw an interesting view in the morning: it snowed at night and
the height of all buildings increased equally! Dino wants to know how many
meters of snow fell. To do this, he went to two neighboring buildings (for
example, 3 - d and 4 - th) and measured their new heights.
Determine how many meters of snow fell if the heights of these buildings equal
to a and b meters respectively.
Input. Two integers a and b (a ≤ b). It is known that the correct answer
always exists, and the height of the fallen snow is no more than 109
meters.
Output. Print the height
of the fallen snow.
|
Sample
input |
Sample
output |
|
11 16 |
1 |
SOLUTION
mathematics
Algorithm analysis
Let Dino measure
the height of snow near buildings with heights 1 + … + i and 1 + … + i + (i + 1). Let x be the height
of the snowfall. Then
a = 1 + … + i + x = (1 + i) * i / 2 + x = (i
+ i2) / 2 + x,
b = 1 + … + i + (i + 1) + x = (2 + i) * (i + 1) / 2 + x = (2 + 3i + i2) / 2 + x
We have: b – a = (2i + 2) / 2 = i + 1, whence i = b – a
– 1. The height of the
snowfall x is a – (i + i2) / 2.
Example
In the sample a = 11, b = 16. Then i = 16 – 11 – 1 =
4. The height of the snowfall is 11 – (4 + 42) / 2 = 11 – 10 = 1.
Algorithm realization
Read the
input data.
scanf("%lld %lld",
&a, &b);
Compute the value of i and the height of the fallen
snow x.
i = b - a - 1;
x = a - i * (i + 1) / 2;
Print the
answer.
printf("%lld\n", x);