9642. Хорошие
пары
Даны два массива А и В, каждый из
которых содержит n чисел. Пара индексов i и j (i < j) называется
хорошей, если выполняется неравенство:
ai + aj > bi
+ bj
Найдите количество таких хороших
пар индексов.
Вход. Первая строка содержит одно целое
число n (n ≤ 105). Вторая строка содержит n
целых чисел – элементы массива А. Третья строка содержит n целых чисел – элементы массива В. Известно, что 0 ≤
ai, bi ≤ 109.
Выход. Выведите одно число – количество
хороших пар индексов.
|
Пример
входа |
Пример
выхода |
|
6 6 5 8 4 7 0 3 5 1 5 2 3 |
11 |
РЕШЕНИЕ
бинарный
поиск
Анализ алгоритма
Перепишем условие ai
+ aj > bi + bj в следующем
виде:
ai – bi > – ( aj – bj)
Построим массив разностей c, в котором ci = ai
– bi. Отсортируем его по возрастанию. Неравенство ai – bi
> – ( aj – bj) эквивалентно ci > – cj, или то же самое что cj > – ci. Это неравенство также можно записать в
виде:
ci + cj > 0
Теперь для
каждого индекса i (0 ≤ i ≤ n – 1) следует найти минимальный
индекс j, такой что cj > – ci. Для всех
индексов k, удовлетворяющих условию j ≤ k ≤ n – 1, пары (i, k) будут хорошими. Однако,
чтобы не учитывать пары дважды, следует выбирать только те из них, для которых k
> i.
Пример
Рассмотрим приведенный
пример. Отсортируем массив ci = ai – bi по возрастанию.
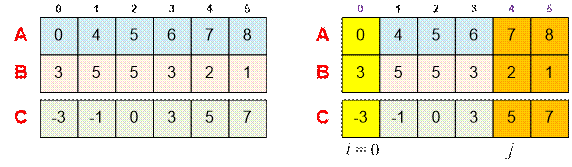
Пусть i = 0. Ищем наименьший индекс j, такой что cj > – c0 = 3. Таким индексом будет j = 4. Следовательно,
пары индексов (0, 4) и (0, 5) будут хорошими.
Пусть i = 1. Ищем наименьший индекс j, такой что cj > – c1 = 1. Таким индексом будет j = 3. Следовательно,
пары индексов (1, 3), (1, 4) и (1, 5) будут хорошими.
Пусть i = 2. Ищем наименьший индекс j, такой что cj > – c2 = 0. Таким индексом будет j = 3. Следовательно,
пары индексов (2, 3), (2, 4) и (2, 5) будут хорошими.
Пусть i = 3. Ищем наименьший индекс j, такой что cj > – c3 = -3. Таким индексом будет j = 1. Пара (i, k) будет хорошей, если
выполняются два условия: k ≥ j и k
> i. В этом случае хорошими являются пары индексов (3, 4) и (3, 5).
Пары (3, 1) и (3, 2) также будут хорошими, но они уже были учтены ранее при
рассмотрении i = 1 (пара (1, 3)) и i = 2 (пара (2, 3)).
Пусть i = 4. Единственной хорошей парой будет (4, 5).
Всего имеется 11
пар хороших индексов.
Реализация алгоритма
Читаем
входные данные.
scanf("%d", &n);
a.resize(n);
b.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
for (i = 0; i < n; i++)
scanf("%d", &b[i]);
Строим
массив разностей c, в котором ci = ai – bi.
c.resize(n);
for (i = 0; i < n; i++)
c[i] = a[i] - b[i];
Сортируем
массив c по возрастанию.
sort(c.begin(),
c.end());
Количество хороших пар индексов
будем подсчитывать в переменной res.
res
= 0;
Перебираем
индексы i.
for (i = 0; i < n; i++)
{
Для
каждого индекса i находим минимальный индекс pos, такой что cpos
> – ci. При этом должно выполняться условие pos ≥
i + 1.
pos =
lower_bound(c.begin() + i + 1, c.end(),-c[i] + 1) - c.begin();
Хорошими
будут все пары индексов (i, k), для которых pos ≤
k ≤ n – 1. Количество таких значений k равно (n
– 1) – pos + 1 = n – pos.
res += n - pos;
}
Выводим
ответ.
printf("%lld\n", res);