9642. Good pairs

You are given two arrays, А and В, each containing n integers. A pair of indices i and j (i < j) is called good if the following inequality holds:

a_i + a_j > b_i + b_j

Find the number of such good pairs of indices.

Input. The first line contains a single integer n (n ≤ 10⁵). The second line contains n integers – the elements of array А. The third line contains n integers – the elements of array В. It is guaranteed that 0 ≤ a_i, b_i ≤ 10⁹.

Output. Print a single integer – the number of good index pairs.

Sample input	Sample output
6 6 5 8 4 7 0 3 5 1 5 2 3	11

SOLUTION

binary search

Algorithm analysis

Let’s rewrite the condition a_i + a_j > b_i + b_j in the following form:

a_i – b_i > – ( a_j – b_j)

Let’s construct an array of differences c, where c_i = a_i – b_i. Sort the array c in non-decreasing order. The inequality a_i – b_i > – ( a_j – b_j) is equivalent to c_i > – c_j, or, equivalently, c_j > – c_i. This inequality can also be written as:

c_i + c_j > 0

Now, for each index i (0 ≤ i ≤ n – 1), we need to find the smallest index j such that c_j > – c_i. For all indices k satisfying j ≤ k ≤ n – 1, the pairs (i, k) will be good. However, to avoid counting pairs twice, we should only consider those for which k > i.

Example

Let’s consider the given example. Sort the array c_i = a_i – b_i in ascending order.

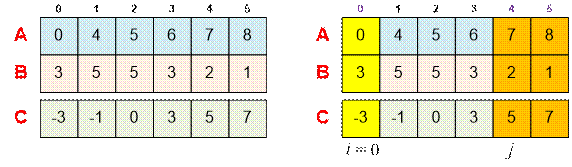
Let’s take i = 0. We are looking for the smallest index j such that c_j > – c₀ = 3. The smallest such index is j = 4. Therefore, the index pairs (0, 4) and (0, 5) are good.

Let’s take i = 1. We are looking for the smallest index j such that c_j > – c₁ = 1. The smallest such index is j = 3. Therefore, the index pairs (1, 3), (1, 4) and (1, 5) are good.

Let’s take i = 2. We are looking for the smallest index j such that c_j > – c₂ = 0. The smallest such index is j = 3. Therefore, the index pairs (2, 3), (2, 4) and (2, 5) are good.

Let’s take i = 3. We are looking for the smallest index j such that c_j > – c₃ = -3. The smallest such index is j = 1. A pair (i, k) is considered good if two conditions are met: k ≥ j and k > i. In this case, the good pairs are (3, 4) and (3, 5). The pairs (3, 1) and (3, 2) are also good, but they have already been counted earlier when considering i = 1 (pair (1, 3)) and i = 2 (pair (2, 3)).

Let’s take i = 4. The only good pair in this case is (4, 5).

In total, there are 11 good index pairs.

Algorithm implementation

Read the input data.

scanf("%d", &n);

a.resize(n); b.resize(n);

for (i = 0; i < n; i++)

scanf("%d", &a[i]);

for (i = 0; i < n; i++)

scanf("%d", &b[i]);

Build an array of differences c, where c_i = a_i – b_i.

c.resize(n);

for (i = 0; i < n; i++)

c[i] = a[i] - b[i];

Sort the array c in ascending order.

sort(c.begin(), c.end());

Count the number of good index pairs in the variable res.

res = 0;

Iterate over the indices i.

for (i = 0; i < n; i++)

{

For each index i, find the smallest index pos such that c_pos > – c_i. At the same time, the condition pos ≥ i + 1 must be satisfied.

pos = lower_bound(c.begin() + i + 1, c.end(),-c[i] + 1) - c.begin();

All index pairs (i, k) such that pos ≤ k ≤ n – 1 will be good. The number of such values of k is (n – 1) – pos + 1 = n – pos.

res += n - pos;

}

Print the answer.

printf("%lld\n", res);