9654. Поиск в
глубину на несвязном графе
Задан неориентированный
несвязный граф. Запустите на нем поиск в глубину. Для каждой вершины выведите
моменты времени, когда она становится серой
/ черной в порядке их первого
посещения.
Вход.
Первая строка содержит количество вершин n
(n ≤ 100) неориентированного графа. Каждая из следующих строк
содержит две вершины a и b – неориентированное ребро графа.
Выход.
Запустите поиск в глубину на графе. Для каждой вершины в отдельной строке выведите моменты
времени, когда она становится серой
/ черной в порядке их первого
посещения.
|
Пример входа |
Пример выхода |
|
6 1 2 5 6 2 4 1 4 |
Vertex: 1, Gray: 1, Black 6 Vertex: 2, Gray: 2, Black 5 Vertex: 4, Gray: 3, Black 4 Vertex: 3, Gray: 7, Black 8 Vertex: 5, Gray: 9, Black 12 Vertex: 6, Gray: 10, Black 11 |
РЕШЕНИЕ
поиск в
глубину
Анализ алгоритма
Построим матрицу
смежности по списку ребер. Запустим поиск в глубину на несвязном графе. Для
каждой вершины v вычислим значения
меток d[v] и f[v]. Затем еще раз
запустим поиск в глубину и в порядке обхода вершин выведем моменты времени, когда она
становится серой / черной.
Пример
Граф, приведенный в
примере, имеет вид:
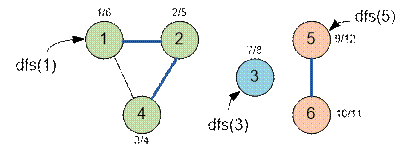
Реализация алгоритма
Объявим матрицу смежности m и рабочие массивы.
#define MAX 101
int m[MAX][MAX], d[MAX], f[MAX], used[MAX];
Поиск в глубину из вершины v. Запоминаем
время входа / выхода из вершины в d[v] / f[v].
void dfs(int v)
{
used[v] = 1;
d[v] = time++;
for (int i = 1; i <= n; i++)
if (m[v][i] && !used[i]) dfs(i);
used[v] = 2;
f[v] = time++;
}
Массивы d
и f уже заполнены. Поиск
в глубину выводит значения меток d[v] / f[v].
void dfs1(int v)
{
used[v] = 1;
printf("Vertex: %d, Gray: %d,
Black %d\n", v, d[v], f[v]);
for (int i = 1; i <= n; i++)
if (m[v][i] && !used[i]) dfs1(i);
}
Основная часть программы. Обнуляем рабочие массивы. Читаем количество
вершин n.
memset(m, 0, sizeof(m)); memset(used, 0, sizeof(used));
scanf("%d", &n);
По списку
ребер строим матрицу смежности.
while (scanf("%d %d", &a, &b) == 2)
m[a][b] = m[b][a] = 1;
Инициализируем время time = 1. Запускаем поиск в
глубину на несвязном графе.
time = 1;
for (i = 1; i <= n; i++)
if (!used[i])
dfs(i);
Следующий поиск в глубину выведет значения меток d[v]
/ f[v] в порядке первого
посещения вершин.
memset(used, 0, sizeof(used));
for (i = 1; i <= n; i++)
if (!used[i]) dfs1(i);
Java реализация
import java.util.*;
public class Main
{
static int g[][], used[], d[], f[];
static int n, m, time = 1;
static void dfs(int v)
{
used[v] = 1;
d[v] = time++;
for(int i = 1; i <= n; i++)
if (g[v][i] == 1
&& used[i] == 0) dfs(i);
f[v] = time++;
used[v] = 2;
}
static void dfs1(int v)
{
used[v] = 1;
System.out.println("Vertex:
" + v + ", Gray " + d[v] + ", Black
" + f[v]);
for (int i = 1; i <= n; i++)
if (g[v][i] == 1
&& used[i] == 0) dfs1(i);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
d = new int[n+1];
f = new int[n+1];
while(con.hasNextInt())
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
time = 1;
for (int i = 1; i <= n; i++)
if (used[i] == 0) dfs(i);
used = new int[n+1];
for (int i = 1; i <= n; i++)
if (used[i] == 0) dfs1(i);
con.close();
}
}