9654. Depth first search on a disconnected graph

Undirected disconnected graph is given. Run depth first search on it. For each vertex print the timestamps when it becomes gray / black in the order of their first visit.

Input. First line contains number of vertices n (n ≤ 100) of undirected graph. Each next line contains two vertices a and b – an undirected edge of the graph.

Output. Run depth first search on a graph. For each vertex print the timestamps when it becomes gray / black in the order of their first visit.

Sample input	Sample output
6 1 2 5 6 2 4 1 4	Vertex: 1, Gray: 1, Black 6 Vertex: 2, Gray: 2, Black 5 Vertex: 4, Gray: 3, Black 4 Vertex: 3, Gray: 7, Black 8 Vertex: 5, Gray: 9, Black 12 Vertex: 6, Gray: 10, Black 11

SOLUTION

depth first search

Algorithm analysis

Construct an adjacency matrix from the list of edges. Run a depth first search on a disconnected graph. For each vertex v, compute the values of the timestamps d[v] and f[v]. Then run the depth first search again and, in the order of traversing the vertices, print the timestamps when it turns gray / black.

Example

Graph given in a sample, has the form:

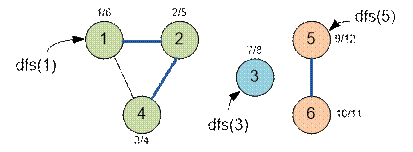
Algorithm realization

Declare an adjacency matrix m and arrays.

#define MAX 101

int m[MAX][MAX], d[MAX], f[MAX], used[MAX];

Depth first search from the vertex v. Remember the entry / exit time to / from the vertex in d[v] / f[v].

void dfs(int v)

{

used[v] = 1;

d[v] = time++;

for (int i = 1; i <= n; i++)

if (m[v][i] && !used[i]) dfs(i);

used[v] = 2;

f[v] = time++;

}

Arrays d and f are already filled. Depth first search prints the values of timestamps d[v] / f[v].

void dfs1(int v)

{

used[v] = 1;

printf("Vertex: %d, Gray: %d, Black %d\n", v, d[v], f[v]);

for (int i = 1; i <= n; i++)

if (m[v][i] && !used[i]) dfs1(i);

}

The main part of the program. Fill with zeroes the arrays. Read the number of vertices n.

memset(m, 0, sizeof(m)); memset(used, 0, sizeof(used));

scanf("%d", &n);

Using the list of edges, construct an adjacency matrix.

while (scanf("%d %d", &a, &b) == 2)

m[a][b] = m[b][a] = 1;

Initialize the time time = 1. Run depth first search on a disconnected graph.

time = 1;

for (i = 1; i <= n; i++)

if (!used[i]) dfs(i);

The next depth first search will print the timestamps d[v] / f[v] in the order of the first visit to the vertices.

memset(used, 0, sizeof(used));

for (i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Java realization

import java.util.*;

public class Main

{

static int g[][], used[], d[], f[];

static int n, m, time = 1;

static void dfs(int v)

{

used[v] = 1;

d[v] = time++;

for(int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs(i);

f[v] = time++;

used[v] = 2;

}

static void dfs1(int v)

{

used[v] = 1;

System.out.println("Vertex: " + v + ", Gray " + d[v] + ", Black " + f[v]);

for (int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs1(i);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

n = con.nextInt();

g = new int[n+1][n+1];

used = new int[n+1];

d = new int[n+1];

f = new int[n+1];

while(con.hasNextInt())

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = g[b][a] = 1;

}

time = 1;

for (int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

used = new int[n+1];

for (int i = 1; i <= n; i++)

if (used[i] == 0) dfs1(i);

con.close();

}

}