9759. ABB
Fernando was hired by the University of
Waterloo to complete a recently started project. The university plans to build
a prestigious street with bungalows outside the campus for important
international guests and staff.
Currently, the street is only partially
developed: it begins at the lakeshore and stretches toward the forest, where it
ends. Fernando’s task is to finish the development of the street by
constructing additional bungalows at its end, near the forest. All the existing
houses are located on one side of the street, and the new bungalows must be
placed on the same side. The existing bungalows differ in type and are painted
in various colors.
In Fernando’s opinion, the street looks
somewhat chaotic. He worries that the new houses, designed in his own style,
might only add to this impression. To bring an element of order, he has decided
to choose the colors of the new bungalows in such a way that the entire color
sequence of houses on the street becomes symmetric. This means that the
sequence of colors should be read the same from both ends of the street.
Among other tasks, Fernando is interested
in finding out the minimum number of new bungalows that must be constructed and
painted accordingly in order to complete the project with the intended
symmetry.
Input. The
first line contains an integer n (1 ≤ n ≤ 4 * 105) – the number of already built
bungalows.
The second line contains a sequence of
their colors, listed in order from the beginning of the street at the lake. It
is a string of length n consisting of lowercase Latin letters from ‘a’ to ‘z’,
each representing a specific color.
Output. Print
the minimum number of bungalows that need to be added to the end of the street
and painted accordingly so that the entire color sequence becomes symmetric.
|
Sample
input 1 |
Sample
output 1 |
|
3 abb |
1 |
|
Sample
input 2 |
Sample
output 2 |
|
12 recakjenecep |
11 |
SOLUTION
z-function
Algorithm analysis
A minimal number of characters must be added to the given
string to turn it into a palindrome.
To do this, we need to find the longest palindromic suffix of
the string, then take the prefix before the start of that palindrome, reverse
it, and append it to the original string.
For example, the longest palindromic suffix of the string abcxqx
is xqx.
The prefix before it is abc. We reverse it (getting cba) and
append it to the original string.
![]()
Consider the string rs = reverse(s)
+ s. Compute the
z-function for this string.
Next, find the smallest index i (such that i
≥ n) for which the equality i + z[i] = 2n
holds. Among such indices, the value z[i] will be maximal. The minimum
number of characters that need to be appended to the original string to form a
palindrome is n – z[i].
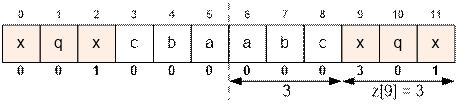
For the string “abcxqx” (length n = 6),
the required index is i
= 9, since 9 + z[9] = 9 + 3 = 12 = 2 * 6.
Example
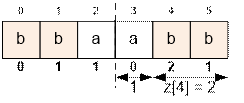
Let’s consider the first example. Compute the z-function for the string reverse(s)
+ s = “bba” + “abb” = “bbaabb”.
The
smallest index i
(i ≥ n) for which the equality i + z[i] = 2n holds is i = 4. Indeed: 4 + z[4] = 4 + 2 = 6 = 2 * 3. Therefore, the answer is
n – z[i] = 3 – 2 = 1. That is, it is enough to add a
single character ‘a’ to the string “abb” to obtain the palindrome
“abba”.
Algorithm implementation
The
function z constructs and returns the z-function for the string s.
vector<int> zfun(string s)
{
int i, l, r, len = s.size();
vector<int> z(len, 0);
l = r = 0;
for (i = 1; i < len; i++)
{
if (i <= r) z[i] = min(r - i + 1, z[i - l]);
while (i + z[i] < len && s[z[i]] == s[i + z[i]]) z[i]++;
if (i + z[i] - 1 > r)
{
l = i;
r = i + z[i] - 1;
}
}
return z;
}
The
main part of the program. Read the input string s.
cin >> n;
cin >> s;
Construct the string rs = reverse(s)
+ s.
rs = s;
reverse(rs.begin(),
rs.end());
rs += s;
Compute the z-function for the string rs.
z = zfun(rs);
Find the smallest index i (i ≥ n)
for which the equality i + z[i] = 2n holds. Among all such
indices, the value of z[i] will be the largest.
for (i = n; i < rs.size(); i++)
if (i + z[i] == 2 *
n)
{
Print the answer.
cout << n - z[i] << endl;
break;
}