ЗАНЯТИЕ 2

 

1. Арифметические и логические операции в языке Си.

1.1. Арифметические операции.

1.2. Логические операции.

1.3. Условный оператор и логические операции.

2. Системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления. Перевод чисел из одной системы счисления в другую.

3. Задачи.

http://www.topcoder.com/tc: SRM 195 (Rounder), SRM 311 (EscapeFromRectangle), SRM 318 (BiggestRectangleEasy), SRM 325 (SalaryCalculator).

 

 

 

1. АРИФМЕТИЧЕСКИЕ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ

 

1.1. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ

 

Основными арифметическими операциями являются: сложение (‘+’), вычитание (‘-‘), умножение (‘*’) и деление (‘/’). Порядок выполнения операций в выражении соответствует их приоритету. Операции с одинаковым приоритетом в выражении выполняются слева направо.

Операция деления (‘/’) выполняется согласно типу ее операндов. Если оба операнда являются целыми числами, то деление будет целочисленным. Если один из операндов является вещественным, то и результат будет вещественным. Например, пусть переменная x имеет целочисленный тип, а y действительный тип. Следующая таблица демонстрирует результаты деления для различных операндов:

 

операция

результат

x = 7 / 3;

x = 2

y = 7 / 3;

y = 2.000000

y = 7.0 / 3;

y = 2.333333

y = (double)7 / 3;

y = 2.333333

 

Рассмотрим второй пример. При выполнении операции присваивания значения выражения переменной, сначала вычисляется значение выражения, а потом оно присваивается переменной. Поскольку операнды во втором примере являются целыми, то результатом деления 7 / 3 будет 2. Потом целочисленное значение 2 преобразовывается в действительное значение 2.000000 и присваивается действительной переменной y.

В четвертом примере перед выполнением операции деления происходит преобразование типа делимого из целого в вещественный. Поэтому деление будет производиться без потери точности.

 

Пример 1.1.1. Найти среднее арифметическое двух целых чисел a и b.

Результатом вычисления выражения (a + b) / 2 может быть действительное число. Поэтому деление должно выполняться с сохранением точности. А для этого один из операндов необходимо преобразовать в действительный тип. Например, результат можно вычислить так: res = (a + b) / 2.0. Программа имеет вид:

 

#include <stdio.h>

int a,b;

double res;

void main(void)

{

  scanf("%d %d",&a,&b);

  res = (a + b) / 2.0;

  printf("%lf\n",res);

}

 

Операция вычисления остатка в Си обозначается символом ‘%’. При этом остаток при делении отрицательного числа на положительное является отрицательным (хотя математически остаток при делении на число n должен лежать в промежутке от 0 до  n – 1 включительно).

 

Операция

результат

x = 6 % 3

x = 0

x = 8 % 3

x = 2

x = -6 % 3

x = 0

x = -8 % 3

x = -2

 

В языке Си при выполнении операций возможны синтаксические сокращения. Например, вместо i = i + 1 можно писать i++. Если <op> – некоторая бинарная операция, то вместо i = i <op>a можно писать i <op>= a.  Примеры сокращений приведены ниже в таблице:

 

операция

сокращение

i = i + 1

i ++

i = i – 1

i --

i = i + a

i += a

i = i % a

i %= a

 

Пример 1.1.2. Временем будем называть пару h : m, где h обозначает количество часов, а m – количество минут. Известно, что в h1 : m1 начался дождь, а в h2 : m2 он закончился (0 £ h1, h2 £ 23, 0 £ m1, m2 £ 59). Необходимо вычислить, сколько времени (hres : mres) шел дождь. Известно, что дождь продолжался не более 24 часов.

Если время h1 : m1 больше чем h2 : m2, то дождь начался в один день, а закончился на следющий. Например, если h1 : m1  = 23:50 и h2 : m2 = 13:20, то дождь длился 13 часов и 30 минут.

Времени h : m соответствует h*60 + m минут, прошедших с полночи. Тогда можно утверждать, что дождь начался в time1 = h1 * 60 + m1 минут, а закончился в time2 = h2 * 60 + m2 минут. Разность между началом и концом дождя составляет timeRes = (time2 – time1  + 24 * 60)  %  (24 * 60) минут. Выделяем количество часов и минут из timeRes и выводим их на экран.

 

#include <stdio.h>

int h1, h2, m1, m2, time1, time2, timeRes, hres, mres;

void main(void)

{

  h1 = 23; m1 = 50;

  h2 = 13; m2 = 20;

  time1 = h1 * 60 + m1; time2 = h2 * 60 + m2;

  timeRes = (time2 - time1 + 24 * 60) % (24 * 60);

  hres = timeRes / 60; mres = timeRes % 60;

  printf("%d:%d\n",hres,mres);

}

 

Упражнение 1.1.1. Имеются одинаковые коробки, каждая из которых вмещает m шаров. Сколько коробок требуется для упаковки n шаров?

 

Упражнение 1.1.2. Рассмотрим условие предыдущей задачи. Сколько коробок будут полностью заполнены, если всего имеется n шаров, а каждая коробка вмещает m шаров?

 

Упражнение 1.1.3. Пусть n – трехзначное число. Присвоить переменным a, b, c соответственно количество сотен, десятков и единиц числа n.

 

 

1.2. ЛОГИЧЕСКИЕ ОПЕРАЦИИ

 

Среди логических операций следует выделить операции ‘и’ (‘and’), ‘или’ (‘or‘), отрицание ‘не’ (‘not’) и сложение по модулю 2 (‘xor’). В языке Си логические операции обозначаются следующим образом:

 

операция

Обозначение в Си

x and y

x && y

x or y

x || y

not x

!x

x xor y

x ^ y

 

Таблицы истинности логических операций приведены в следующих таблицах:

 

x

y

x and y

 

x

y

x or y

 

x

not x

 

x

y

x xor y

0

0

0

 

0

0

0

 

0

1

 

0

0

0

0

1

0

 

0

1

1

 

1

0

 

0

1

1

1

0

0

 

1

0

1

 

 

 

 

1

0

1

1

1

1

 

1

1

1

 

 

 

 

1

1

0

 

Следует отметить также логическую операцию сравнения, обозначаемую в Си двумя знаками равенства. При этом выражение (x == y) эквивалентно  !(x xor y). Операция называется операцией “сложение по модулю 2”, потому что x xor y = (x + y) mod 2. Логические операции подчиняются правилу Де-Моргана:

not (x and y) = (not x) or (not y)

или то же самое

!(x && y) = !x || !y

 

Упражнение 1.2.1. Составить таблицу истинности следющих функций:

1. Равенства: x = y;

2. Импликации: x É y = (not x) or y

 

 

1.3. УСЛОВНЫЙ ОПЕРАТОР И ЛОГИЧЕСКИЕ ОПЕРАЦИИ

 

Используя логические операции, можно строить условные выражения. Например, реализуем на языке Си следующие задачи, в которых требуется написать выражения для условного оператора.

 

Пример 1.3.1. Проверить, лежит ли значение переменной x в интервале (1; 5):

if ((x > 1) && (x < 5)) ...

Пример 1.3.2. Проверить, лежит ли значение переменной x вне интервала (1; 5):

if ((x <= 1) || (x >= 5)) ...

 

В языке Си нет булевого типа. Если значение переменной равно 0, то ее значение считается равным ‘ложь’ (иначе ‘истина’). Так, например, вместо выражения

if (x == 0) ...

можно писать

if (!x) ...

Выражение !x будет истинным, когда x будет ложным. А это возможно лишь в случае, когда x равно нулю.

 

Пример 1.3.3. Записать условие того, что обе переменные x и y имеют значение 0:

if ((x == 0) && (y == 0)) ...

или то же самое

if (!x && !y) ...

 

Упражнение 1.3.1. Записать условие того, что переменная х принимает одно из значений множества S = {1, 3, 6}.

 

Истинное выраженние считается равным 1, ложное выражение считается равным нулю.

 

Пример 1.3.4. Присвоим целочисленным переменным значения логических выражений и выведем их.

 

#include <stdio.h>

int i;

void main(void)

{

  i = (3 > 4);

  printf("%d\n",i);      // 0

  i = (3 < 4);

  printf("%d\n",i);      // 1

}

 

Пусть f(x) и g(x) – некоторые функции, p(x) – предикат. Расмотрим функцию:

Функцию y(x) можно реализовать без использования структуры if … else … .  Учитывая значения логических выражений, можно записать:

y(x) = f(x) * p(x) + g(x) * (1 – p(x))

Записи 1 – p(x) и !p(x) эквивалентны.

 

Пример 1.3.5. Вычислить значение функции:

y(x) =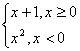

 

#include <stdio.h>

double x, y;

void main(void)

{

  scanf("%lf",&x);

  y = (x + 1) * (x >= 0) + (x * x) * (x < 0);

  printf("%lf\n",y);

}

 

Пример 1.3.6. Вычислить значение функции знака числа:

sgn(x) =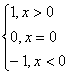

Запишем функцию в виде:

sgn(x) = 1 * (x > 0) + 0 * (x = 0) + (-1) * (x < 0) = (x > 0) – (x < 0)

 

#include <stdio.h>

int x, y;

void main(void)

{

  scanf("%d",&x);

  y = (x > 0) - (x < 0);

  printf("%d\n",y);

}

 

 

2. СИСТЕМЫ СЧИСЛЕНИЯ

 

В повседневной жизни мы пользуемся десятичной системой счисления, которая имеет 10 цифр: 0, 1, …, 8, 9. Каждое натуральное число n =  можно представить в виде

n = an * 10n + an-1 * 10n-1 + … + a1 * 10 + a0

Например, 123 = 1 * 102 + 2 * 101 + 3 * 100.

 

В двоичной системе счисления пользуются лишь двумя цифрами: 0 и 1. В восьмеричной – цифрами от 0 до 7, а в шестнадцатеричной – цифрами от 0 до 9 и буквами от ‘A’ до ‘F’, которые соответствуют числам от 10 до 15. В следующей таблице показаны записи чисел от 1 до 16 в разных системах счисления:

 

десятичная

двоичная

восьмеричная

шестнадцатеричная

1

1

1

1

2

10

2

2

3

11

3

3

4

100

4

4

5

101

5

5

6

110

6

6

7

111

7

7

8

1000

10

8

9

1001

11

9

10

1010

12

A

11

1011

13

B

12

1100

14

C

13

1101

15

D

14

1110

16

E

15

1111

17

F

16

10000

20

10

 

Если b – основание системы счисления, то числу n, имеющему в ней запись , в десятичной системе соответствует число

n = an * bn + an-1 * bn-1 + … + a1 * b + a0

Примеры перевода чисел из разных систем счисления в десятичную:

1. 1111 из двоичной: 11112 = 1 * 23 + 1 * 22 + 1 * 21 + 1 = 1510

2. 16 из восьмеричной: 168 = 1 * 81 + 6 = 1410

3. FF из шестнадцатеричной: FF16 = 15 * 161 + 15 = 25510

 

Для перевода из десятичной системы счисления в двоичную (восьмеричную, шестнадцатеричную, …) пользуются делением в столбик. При делении числа n на 2 под числом n записываем остаток от деления n на 2, под двойкой – частное. Процесс деления оканчиваем, когда частное станет равным 1. Далее следует записать последнее частное (единицу) и все остатки от деления в обратном порядке. Например, найдем двоичное представление числа 20:

20

2

 

 

 

0

10

2

 

 

 

0

5

2

 

 

 

1

2

2

 

 

 

0

1

Записав остатки в обратном порядке, получим: 2010 = 101002.

 

Найдем шестнадцатеричное представление числа 511:

511

16

 

15 = F

31

16

 

15 = F

1

Из таблицы получим: 51110 = 1FF16.

 

При умножении на 10 в десятичной системе счисления к числу приписывается справа 0. Например, 71 * 10 = 710. Аналогично при умножении на b числа n в b - значной системе счисления к числу n приписывается справа 0. Например:

5 * 2 = 10, в двоичной системе счисления: 1012 * 210 = 10102;

255 * 162 = 65280, в шестнадцатеричной системе счисления: FF16 * 1610 * 1610 = FF0016;

 

Упражнение 2.1. Найти двоичное, восьмеричное и шестнадцатеричное представление десятичного числа 31.

 

Упражнение 2.2. Найти двоичное представление следующих чисел:

а) 22 + 24            б) 26 – 1           в) 3 * 82

 

 

3. ЗАДАЧИ

 

При сдаче задач на Топкодере следует писать функцию – метод класса. Например, рассмотрим две достаточно простые задачи с объяснениями и реализацией.

 

Матч 195, Округление (Rounder)

Дивизион 2, Уровень 1

 

Для заданного числа n найти ближайшее целое, которое делится на b. Если таких чисел несколько, то найти наибольшее.

 

Класс: Rounder

Метод: int round(int n, int b)

Ограничения: 1 £ n £ 106, 2 £ b £ 500.

 

Вход. Два числа n и b.

 

Выход. Ближайшее целое к n, которое делится на b. Если n находится строго посредине двух чисел, делящихся на b, то вернуть наибольшее.

 

Пример входа

n

b

5

10

4

10

100

3

49

7

 

Пример выхода

10

0

99

49

 

РЕШЕНИЕ

Ближайшим к n целым, делящимся на b, будет число  . Если n находится строго посредине двух чисел, делящихся на b, это значение будет наибольшим среди них. В языке Си выражение примет вид: (n + b / 2) / b * b.

Класс Rounder и метод round имеют следующий вид:

 

#include <stdio.h>

class Rounder

{

public:

  int round(int n, int b)

  {

    return ((n + (b / 2)) / b) * b;

  }

};

 

Заметим, что после объявления класса следует ставить точку с запятой. Методом называется функция, объявленная в классе. Функцию следует объявить публичной (public) для того чтобы ее можно было вызывать извне. Именно в таком виде следует сдавать задачу на Топкодере.

Для тестирования метода следует написать функцию main. Она должна содержать создание экземпляра класса, вызов метода с конкретными входными данными и вывод результата. Для задачи Rounder функция main имеет вид:

 

void main(void)

{

  Rounder s;

  int res = s.round(123456,7);

  printf("%d\n",res);

}

 

Матч 325, Калькулятор зарплаты (SalaryCalculator)

Дивизион 2, Уровень 1

 

Работая в компании, за первые 200 часов работник получает зарплату в размере p1 долларов в час каждый месяц. За остальные часы до конца месяца ставка работника составляет p2 долларов в час. Вычислить, какое наименьшее количество часов должен работать работник в месяц, чтобы получить суммарную зарплату в salary долларов.

 

Класс: SalaryCalculator

Метод: double calcHours(int p1, int p2, int salary)

Ограничения: 1 £ p1, p2 £ 100, 1 £ salary £ 106.

 

Вход. Ежемесячная зарплата работника в час за первые 200 часов и за последующие часы.

 

Выход. Наименьшее количество часов должен работать работник в месяц, чтобы получить суммарную зарплату в salary долларов.

 

Пример входа

p1

p2

salary

10

15

1000

10

15

3000

82

8

12140

 

Пример выхода

100.0

266.6666666666667

148.0487804878049

 

РЕШЕНИЕ

 

За 200 часов работник получит t = p1 * 200 долларов. Если эта сумма больше salary, то достаточно работать salary / p1 часов. Иначе следует отработать 200 часов с зарплатой p1 долларов в час, а остальное время с зарплатой p2 долларов в час. При этом количество часов, когда зарплата будет составлять p2 долларов в час, равна (salary – t) / p2.

 

#include <stdio.h>

class SalaryCalculator

{

public:

  double calcHours(int p1, int p2, int salary)

  {

    int t = p1 * 200;

    if (t >= salary) return 1.0 * salary / p1;

    return 200 + 1.0 * (salary - t) / p2;

  }

};

 

Для тестирования функции calcHours следует написать функцию main. Напомним, что при сдаче задачи на Топкодере функцию main приводить не следует (следует сдавать только код класса).

 

void main(void)

{

  SalaryCalculator s;

  double res = s.calcHours(82,8,12140);

  printf("%lf\n",res);

}

 

Матч 311, Убежать из прямоугольника (EscapeFromRectangle)

Дивизион 2, Уровень 1

 

Вы находитесь в точке (x, y) внутри прямоугольника, нижний левый угол которого имеет координаты (0, 0), а правый верхний (w, h). Найти наименьшее расстояние, которое Вам следует преодолеть чтобы достичь границы прямоугольника.

 

Класс: EscapeFromRectangle

Метод: int shortest(int x, int y, int w, int h)

Ограничения: 2 £ w, h £ 1000, 1 £ x £ w-1, 1 £ y £ h-1.

 

Вход. Целочисленные координаты Вашего положения (x, y) и правой верхней вершины прямоугольника (w, h).

 

Выход. Наименьшее расстояние, которое следует преодолеть для достижения границы прямоугольника.

 

Пример входа

x

y

w

h

1

1

5

5

653

375

1000

1000

161

181

762

375

 

Пример выхода

1

347

161

 

РЕШЕНИЕ

 

Находим расстояния от точки (x, y) до всех четырех сторон прямоугольника, которые соответственно равны x, y, w – x, h – y. Возвращаем наименьшее из этих значений.

 

#include <stdio.h>

class EscapeFromRectangle

{

public:

  int shortest(int x, int y, int w, int h)

  {

    int res = x;

    if(y < res) res = y;

    if(w - x < res) res = w - x;

    if(h - y < res) res = h - y;

    return res;

  }

};

 

Далее при разборах задач с Топкодера функцию main приводить не будем.

 

Матч 318, Наибольший прямоугольник (BiggestRectangleEasy)

Дивизион 2, Уровень 1

 

У Джона есть n спичек, каждая из которых имеет длину 1. Он хочет составить из них прямоугольник наибольшей площади. Ломать спички нельзя. Джону не обязательно использовать все спички.

 

Класс: BiggestRectangleEasy

Метод: int findArea(int n)

Ограничения: 4 £ n £ 10000.

 

Вход. Количество спичек n, которое имеется в наличии у Джона.

 

Выход. Наибольшая площадь прямоугольника, который может составить Джон при помощи имеющихся у него спичек.

 

Пример входа

n

11

5

7254

 

Пример выхода

6

1

3288782

 

РЕШЕНИЕ

 

Если одна из сторон прямоугольника равна x, то другую можно найти по формуле:

y = (n – 2*x) / 2

Площадь полученного прямоугольника равна S(x) = x * (n – 2*x) / 2. Она будет наибольшей в такой точке x, в которой S’(x) = 0. Имеем: S’(x) = (n – 4*x) / 2 = 0, x = n / 4. То есть искомым прямоугольником будет квадрат.

Если n не делится на 4, то выполняя целочисленные деления, получим правильный результат.

 

#include <stdio.h>

class BiggestRectangleEasy

{

public:

  int findArea(int n)

  {

    int x = n / 4;

    int y = (n - 2 * x) / 2;

    return x * y;

  }

};

 

 

УКАЗАНИЯ К РЕШЕНИЮ УПРАЖНЕНИЙ

 

Упражнение 1.1.1. Ответом будет значение выражения , которое на языке Си можно записать в виде (m + n – 1) / n.

 

Упражнение 1.1.2. Ответом будет значение выражения , которое на языке Си можно записать в виде m / n.

 

Упражнение 1.1.3. Следует выполнить следующие операции:

a = n / 100; b = n / 10 % 10; c = n % 10;

 

Упражнение 1.2.1. Таблицы истинности равенства и импликации имеют вид:

 

x

y

x = y

 

x

y

x É y

0

0

1

 

0

0

1

0

1

0

 

0

1

1

1

0

0

 

1

0

0

1

1

1

 

1

1

1

 

Упражнение 1.3.1. Выражение имеет вид:

if ((x == 1) || (x == 3) || (x == 6)) . . .

 

Упражнение 2.1. 3110 = 111112, 3110 = 378, 3110 = 1F16.

 

Упражнение 2.2.Ответами будут следующие значения:

а) 22 + 24 = 101002        б) 26 – 1 = 1111112     в) 3 * 82 = 110000002