ЗАНЯТИЕ
3
1. Операторы цикла: синтаксис и
семантика.
1.1. Оператор for.
1.2.
Оператор while.
1.3.
Оператор do-while.
2. Многократный ввод-вывод. Понятие
однократного и многократного ввода-вывода. Чтение данных до конца файла.
Возвращаемое значение функции scanf.
3. Форматированный ввод-вывод. Формат целочисленных и вещественных данных.
4. Математические функции. Библиотека <math.h>.
Алгебраические и тригонометрические
функции. Функции округления. Вычисление степени числа. Константа 
.
5. Задачи
http://acm.uva.es/problemset: 113 (Сила криптографии), 408 (Однородный генератор), 10127 (Единицы), 10509
(Обмануть Мистера Фреймана), 10633 (На редкость простая задача), 10683
(Десятичные часы), 10773 (Назад к
математике средней школы), 10783 (Сумма нечетных чисел), 10784 (Диагональ).
http://acm.timus.ru: 1068 (Sum).
http://www.topcoder.com/tc: SRM 326 (AdditionCycles), SRM 343
(PersistentNumber),
TCHS 29 (ReverseSums).
1. ОПЕРАТОРЫ ЦИКЛА
Язык Си имеет три конструкции,
реализующие операторы цикла: for, while, do-while.
1.1. ОПЕРАТОР for
Цикл for является одним из
основных видов циклов, которые имеются во всех универсальных языках
программирования, включая С. Однако
версия цикла for, используемая в С, обладает большей мощностью и гибкостью.
Основная идея
функционирования for заключается в том, что операторы, находящиеся внутри цикла,
выполняются фиксированное число раз, в то время как переменная цикла (известная
еще как индексная переменная) пробегает определенный ряд значений.
Синтаксис:
for (<выражение инициализации>; <условное выражение>;
<выражение цикла>)
<тело оператора>;
Параметры цикла for,
заключенные в скобки, должны разделяться точкой с запятой (позиционный
параметр), которая делит в свою очередь пространство внутри скобок на три
сектора.
Тело оператора
for выполняется нуль и более раз до тех пор, пока условное
выражение <условное выражение> не станет
ложным.
Выражения инициализации
<выражение инициализации> и цикла <выражение цикла> могут быть
использованы для инициализации и модификации величин во время выполнения
оператора for.
Первым шагом при
выполнении оператора for является вычисление выражения
инициализации, если оно имеется. Далее вычисление продолжается в зависимости от
значения условного выражения:
1. Если условное выражение
истинно (не равно нулю), то выполняется тело оператора. Потом вычисляется выражение
цикла (если оно есть). Процесс повторяется снова с вычислением условного
выражения.
2. Если условное выражение опущено, то его
значение принимается за истину и процесс выполнения продолжается, как описано
выше. В этом случае оператор for может завершиться только при выполнении
в теле оператора операторов break, goto, return.
3. Если условное выражение ложно,
то выполнение оператора for заканчивается и управление
передается следующему оператору в программе.
Оператор for может
завершиться при выполнении
операторов break, goto, return в теле оператора.
В некоторых случаях использование оператора запятая (,) позволит вводить
составные выражения в оператор цикла for.
Пример 1.1.1. Вычислить сумму чисел от 1 до
100.
for (s=0,i=1;i<=100;i++)
s = s + i;
Выражение инициализации обнуляет
переменную суммы s и присваивает 1
переменной i. Операторы, записанные
через запятую, выполняются последовательно. Выражение цикла прибавляет 1 к
переменной i, а в теле цикла
происходит суммирование переменных s
и i. Цикл завершает свою работу когда
переменная i достигнет значения 101.
То есть последним числом, которое будет прибавлено к переменной s, будет 100. В конце работы оператора for
переменная s будет содержать число
5050 – сумму натуральных чисел от 1 до 100.
Пример 1.1.2. Тело цикла, которое не
выполняется
for (s=0,i=1;i<1;i++)
s = s + i;
Если в предыдущей программе
заменить условное выражение на i <
1, то тело цикла никогда не выполнится. После инициализации s = 0, i = 1 будет проверено условное выражение i < 1. И поскольку оно ложно, то управление программой перейдет
на следующий за for оператор.
Пример 1.1.3. Для
заданного натурального n вычислить
сумму
S = 
+ 
+ … + 
Сумму
будем вычислять в переменной s, имеющей тип double. Каждое слагаемое имеет
вид 
, где 1 £ i £ n. На языке Си это выражение можно записать как 1.0 / (i * (i
+ 1)) или как 1.0 / i / (i + 1). В качестве числительного следует
писать 1.0, а не 1, так как результат деления должен быть действительным. В
цикле последовательно прибавляем к нулю все слагаемые 1.0 / i / (i
+ 1) для i от 1 до n.
#include <stdio.h>
int i,n;
double s;
void main(void)
{
scanf("%d",&n);
s = 0;
for(i=1;i<=n;i++)
s += 1.0 / i / (i+1);
printf("%lf\n",s);
}
Указанную сумму можно также
вычислить непосредственно. Заметив, что
= 
– 
можно получить:
S = + + … + = 
– 
+ – 
+ . . . + 
– 
= 1 –
Пример 1.1.4 [Вальядолид, 10127]. Единицы.
Дано натуральное число n (0 £ n £ 10000), которое не делится ни на 2, ни на 5. Существуют числа, которые
состоят только из единиц и делятся на n.
Найти количество единиц в минимальном таком числе.
|
Пример входа |
Пример выхода |
|
3 7 9901 |
3 6 12 |
Для числа n = 3 наименьшим числом, состоящим из одних единиц и которое
делится на 3, будет 111. Для n = 7
таким числом будет 111111.
Построим последовательность чисел
a1 = 1, ai = (10*ai-1
+ 1) mod 10. ai содержит остаток от деления числа, состоящего
из i единиц, на n. Как только
для некоторого i значение ai станет равным 0,
останавливаем итерационный процесс. Число, состоящее из i единиц,
делится нацело на n.
#include <stdio.h>
void main(void)
{
int n, one, count_ones;
for(;scanf("%d",&n) == 1;)
{
for(one = 1, count_ones = 1; one > 0; count_ones++)
one = (10 * one + 1) % n;
printf("%d\n",count_ones);
}
}
Упражнение 1.1.1. Вычислить значение произведения
* 
* 
* … * 
для заданного n при помощи цикла for и непосредственно при помощи математических
преобразований.
1.2. ОПЕРАТОР while
В конструкции while
вычисляется выражение. Если его значение отлично от нуля (истинно), то
выполняется тело оператора и выражение вычисляется снова. Этот цикл
продолжается до тех пор, пока значение выражения не станет нулем, после чего
выполнение программы продолжается с места после тела оператора.
Синтаксис:
while (<выражение>) <тело
оператора>;
Пример 1.2.1. Вычислить сумму чисел от 1 до
100.
#include <stdio.h>
int s, i;
void main(void)
{
s = 0; i = 100;
while(i >
0)
{
s = s + i;
i--;
}
printf("%d\n",s);
}
Изначально значение суммы s положили равным нулю. В переменной i содержится очередное слагаемое,
которое будет прибавляться к сумме s.
Первым таким слагаемым будет i = 100.
Пока выражение, заключенное в круглые скобки цикла while будет истинным,
совершается тело цикла. В теле цикла к сумме s прибавляется слагаемое i
и это слагаемое уменьшается на 1. Цикл закончит свое выполнение, когда
слагаемое i станет равным нулю и не
будет выполняться условие i > 0.
Операторы можно разделять запятой
(‘,’), тогда они будут выполняться последовательно. Если два оператора в теле
цикла while объединить в последовательное выполнение, то можно не брать в
фигурные скобки тело цикла:
#include <stdio.h>
int s, i;
void main(void)
{
s = 0; i = 100;
while(i >
0)
s += i, i--;
printf("%d\n",s);
}
Упражнение 1.2.1 [Топкодер, SRM 343, PersistentNumber].
По заданному
числу х определим функцию p(x), равную произведению его цифр.
Образуем последовательность x, p(x), p(p(x)), … . Стойкостью числа x
назовем наименьший индекс однозначного числа в указанной последовательности.
Нумерация индексов в последовательности начинается с нуля. Например, для x = 99 имеем: p(99) = 9 * 9 = 81, p(81) = 8 * 1 = 8. Стойкость числа 99 равна 2.
Класс: PersistentNumber
Метод: int getPersistence(int n)
Ограничения:
0 £ n £ 2 * 109.
Вход. Целое число n.
Выход. Стойкость числа n.
Пример входа
|
n |
|
99 |
|
268 |
|
86898 |
Пример выхода
2
4
7
Упражнение 1.2.2 [Топкодер, TCHS 29, ReverseSums].
Для нахождения
обратной суммы следует сложить заданное число с числом, цифры которого идут в
обратном порядке. Например, для числа 1325
результатом будет 1325 + 5231 = 6556.
Класс: ReverseSums
Метод: int getSum(int n)
Ограничения:
1 £ n
£ 99999.
Вход. Натуральное число n.
Выход. Сумма заданного числа с обратным.
Пример входа
|
n |
|
1325 |
|
100 |
|
1 |
Пример выхода
6556
101
2
1.3. ОПЕРАТОР do-while
Оператор цикла do-while
проверяет условие окончания в конце, после каждого прохода через тело цикла;
тело цикла всегда выполняется по крайней мере один раз. Сначала выполняется
тело оператора, затем вычисляется выражение. Если оно истинно, то тело
оператора выполняется снова и т.д. Если выражение становится ложным, цикл
заканчивается.
Синтаксис:
do <тело оператора> while
(<выражение>);
Тело оператора do
выполняется один или несколько раз до тех пор, пока выражение
<выражение> станет ложным
(равным нулю). Вначале выполняется <тело оператора>, затем
вычисляется <выражение>. Если выражение ложно, то оператор do завершается и управление передается
следующему оператору в программе.
Если выражение истинно
(не равно нулю), то тело оператора выполняется снова и снова проверяется
выражение. Выполнение тела
оператора продолжается до тех пор,
пока выражение не станет ложным.
Пример 1.3.1. Вычислить сумму чисел от 1 до
100.
#include <stdio.h>
int s, i;
void main(void)
{
s = 0; i = 100;
do {
s = s
+ i;
i--;
} while(i
> 0);
printf("%d\n",s);
}
В переменной s накапливается сумма, переменная i принимает все значения от 100 до 1. В теле цикла происходит
прибавление значения i к сумме s и уменьшение i на 1. Цикл повторяется пока выражение (i > 0) истинно. Как только значение переменной i станет равным 0, цикл завершается и
управление передается следующей команде.
Упражнение 1.3.1 [Топкодер, SRM 326, AdditionCycles]. Имеется число n в
границах от 00 до 99, записанное двумя цифрами (если число меньше 10, то перед
ним стоит ведущий 0). Сложим цифры числа. Припишем к правой цифре первого числа
правую цифру суммы и получим новое число. Если повторять несколько раз
описанную процедуру, то снова можно получить n. Например:
|
число |
сумма цифр |
конкатенация цифр |
|
26 |
2 + 6 = 8 |
68 |
|
68 |
6 + 8 = 14 |
84 |
|
84 |
8 + 4 = 12 |
42 |
|
42 |
4 + 2 = 06 |
26 |
По заданному числу n
следует найти количество шагов описанных преобразований, через которое можно
снова получить n.
Класс: AdditionCycles
Метод: int cycleLength(int n)
Ограничения:
0 £ n £ 99.
Вход. Целое число n.
Выход. Число шагов преобразований, после выполнения которых снова
появится число n.
Пример входа
|
n |
|
26 |
|
55 |
|
0 |
Пример выхода
4
3
1
2. МНОГОКРАТНЫЙ
ВВОД – ВЫВОД
При решении олимпиадных задач
различают однократный ввод (single input) и многократный ввод (multiple input).
Однократный ввод характеризуется данными для одного теста. Если на вход
подаются данные для нескольких тестов, то говорят о многократном вводе.
Рассмотри два примера.
Пример 2.1. На вход подаются два числа a и b. Найти их сумму.
Для решения задачи достаточно
ввести два числа, найти их сумму и вывести результат (занятие 1, раздел 2.3).
Пример 2.2. На вход подаются несколько строк. Первая строка содержит
количество тестов n. Каждая из
следующих n строк содержит два числа a и b.
Для каждого теста найти сумму двух чисел и вывести ее в отдельной строке.
Читаем в переменную n количество тестов. Далее в цикле для
каждой входной строки вводим слагаемые a
и b, находим их сумму и выводим на
экран.
#include <stdio.h>
int i, a, b, n;
void main(void)
{
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d
%d",&a,&b);
printf("%d\n",a + b);
}
}
Цикл можно организовать и при
помощи конструкции while. В таком случае вводить дополнительную переменную i нет необходимости:
#include <stdio.h>
int a, b, n;
void main(void)
{
scanf("%d",&n);
while(n--)
{
scanf("%d
%d",&a,&b);
printf("%d\n",a + b);
}
}
Цикл while будет продолжаться
до тех пор, пока выражение n-- будет
оставаться истинным. А это будет выполняться до тех пор, пока n не станет равным 0.
Пример 2.3. На вход подаются несколько строк. Каждая строка содержит два
числа a и b. Для каждой строки вывести сумму двух чисел, находящихся в ней.
Условие задачи отличается от
предыдущей тем, что мы не знаем количество входных строк. В таком случае
следует читать данные до конца файла. В отличии от языка Паскаль, в Си в таком
случае не следует прибегать к файловым операторам.
Функция scanf не только вводит
данные, но и возвращает целочисленное значение, равное количеству прочитанных
аргументов. То есть если записать выражение
i = scanf("%d %d",&a,&b);
и ввести два числа a и b,
то переменная i примет значение 2.
Это свойство функции очень удобно использовать при чтении данных до конца
файла. Дело в том, что если программа прочитает все данные и дойдет до конца
файла, то при следующем вызове функции scanf она вернет значение, равное
-1. Решение примера 3.2.3 имеет вид:
#include <stdio.h>
int a, b;
void main(void)
{
while(scanf("%d %d",&a,&b) == 2)
printf("%d\n",a
+ b);
}
В цикле while читаем два числа a и b.
Пока вводятся два числа, scanf возвращает 2 и выполняется
тело цикла (печать суммы чисел). Кодга дойдем до конца файла, функция scanf
не сможет прочитать следующие два числа и вернет -1. Выполнение цикла
закончится.
Напоминание! При чтении данных с консоли ввести символ “конец файла”
можно, нажав комбинацию клавиш ^Z.
Пример 2.4. На вход подаются несколько строк. Каждая строка содержит два
неотрицательных целых числа a и b. Для каждой строки вывести сумму двух
чисел, находящихся в ней. Последняя строка содержит два нуля и не
обрабатывается.
Пример отличается от предыдущего
тем, что окончание работы цикла следует произвести не по достижению конца
файла, а при прочтении значений a =
0, b = 0.
#include <stdio.h>
int a, b;
void main(void)
{
while(scanf("%d %d", &a, &b), a + b)
printf("%d\n", a + b);
}
Условное выражение цикла while
состоит из двух частей: функции scanf и выражения a + b.
Цикл продолжается до тех пор, пока оба выражения остаются истинными. Очевидно,
что функция scanf всегда будет возвращать 2 (поскольку до конца файла при
обработке данных в этой задаче мы не дойдем), а значение a + b будет оставаться
истинным пока оба значения a и b не станут равными 0 (по условию a и b
целые неотрицательные).
Напоминание! Арифметическое выражение является истинным, если оно не
равно 0.
Упражнение 2.1 [Вальядолид, 10633]. На редкость простая
задача. N –
некоторое целое число, имеющее в десятичной записи хотя бы две цифры. Джон
производит над этим числом следующую операцию: он зачеркивает последнюю цифру,
получает число M и вычисляет N – M. Зная значение N – M, следует найти N.
Вход. Каждая строка содержит целое положительное число, являющееся
значением N – M (10 £ N – M £ 1018).
Последняя строка содержит 0 и не обрабатывается.
Выход. Для каждого входного значения N – M вывести все возможные N в возрастающем
порядке. Числа в одной строке следует разделять одним пробелом.
|
Пример входа |
Пример выхода |
|
18 |
19 20 |
|
0 |
|
Упражнение 2.2 [Вальядолид, 10783]. Сумма нечетных чисел. Вычислить сумму всех нечетных чисел из интервала [a,
b]. Например, сумма нечетных чисел из интервала [3, 9] равна 3 + 5 + 7 +
9 = 24.
Вход. Первая строка содержит количество тестов T (1 £ T £ 100). Каждый тест состоит из двух чисел a и b (0 £ a £ b £ 100), каждое из которых находится в отдельной строке.
Выход. Для каждого теста вывести его номер и сумму всех нечетных
чисел из интервала [a, b].
|
Пример входа |
Пример выхода |
|
2 |
Case 1: 9 |
|
1 |
Case 2: 8 |
|
5 |
|
|
3 |
|
|
5 |
|
Упражнение 2.3 [Тимус, 1068]. Сумма. Найти сумму чисел от 1 до n включительно.
Вход. Целое число n, не
большее 10000 по абсолютному значению.
Выход. Сумма чисел от 1 до n включительно.
|
Пример входа |
Пример выхода |
|
-3 |
-5 |
3. ФОРМАТИРОВАННЫЙ
ВВОД-ВЫВОД
В первом уроке были приведены форматы
ввода-вывода элементарных типов данных. Формат позволяет выводить числовые
значения переменных с определенным количеством знаков. Следующая таблица
описывает форматы данных:
|
тип |
формат |
|
int |
%<n>d |
|
float |
%<n>.<m>f |
|
double |
%<n>.<m>lf |
Здесь <n> и <m> –
некоторые целые неотрицательные числа. Значение переменной выводится в
<n> позициях. При выводе значения действительного типа после десятичной
запятой выводится <m> знаков, десятичная точка занимает одну позицию.
Если <n> больше чем количество цифр в выводимом значении, то перед числом
выводятся пробелы. Если <n> меньше чем количество цифр в выводимом
значении, то значение выводится с таким количеством цифр, которое оно содержит.
|
переменная |
формат
вывода |
выводимое
значение |
|
int a = 456 |
%1d |
456 |
|
int a = 456 |
%3d |
456 |
|
int a = 456 |
%5d |
456 |
|
float f =
34.1223 |
%3.2f |
34.12 |
|
float f =
34.1223 |
%7.3f |
34.122 |
|
float f =
34.1223 |
%8.4f |
34.1223 |
|
float f =
34.1223 |
%9.4f |
34.1223 |
|
double d =
1.123456789 |
%5.3lf |
1.123 |
|
double d =
1.123456789 |
%7.5lf |
1.12346 |
|
double d =
1.123456789 |
%12.9lf |
1.123456789 |
|
double d =
1.123456789 |
%15.11lf |
1.12345678900 |
Если <m> = 0, то
действительное число при выводе округляется до целого значения.
Пример 3.1. Вывести таблицу умножения 9*9. Каждое число в таблице должно
занимать две позиции, между числами в одной строке должен находиться один
пробел.
Приведенный пример показывает,
как можно форматировать табличный вывод. Используя двойной цикл, построчно
выводим требуемую таблицу.
for(i = 1; i < 10; i++)
{
for(j = 1; j < 10; j++)
printf("%2d
", i*j);
printf("\n");
}
Пример 3.2. Входная строка задает дату и имеет формат: “DD:MM:YYYY”
(день:месяц:год). Необходимо в три разные переменные занести день, месяц и год.
int day,month,year;
scanf("%d:%d:%d",&day,&month,&year);
Пример 3.3. На вход подается квадратная
матрица размером n * n (n < 10), каждый элемент которой представляет собой цифру. Первая строка задает n, следующие строки описывают
матрицу. Необходимо найти сумму всех чисел матрицы.
|
Пример входа |
Пример выхода |
|
3 111 222 333 |
18 |
Для чтения однозначных чисел
следует воспользоваться форматом “%1d”:
#include <stdio.h>
int s, d, n, i, j, m[10][10];
int main(void)
{
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
scanf("%1d", &d);
s += d;
}
printf("%d\n", s);
return 0;
}
Упражнение 3.1 [Вальядолид, 408].
Однородный генератор. Псевдослучайные числа можно сгенерировать при помощи формулы:
seed(x
+ 1) = (seed(x) + STEP) % MOD,
где % – операция взятия остатка.
Недостаток такого метода получения случайных чисел состоит в том, что
циклически будет генерироваться одна и та же последовательность. Например, если
STEP = 3 и MOD = 5, то циклически будет повторяться последовательность 0, 3, 1,
4, 2. Если STEP = 15 и MOD = 20, то получим серию чисел 0, 15, 10, 5.
Выяснить, можно при помощи такого
генератора получить все числа от 0 до MOD – 1.
Вход. Каждая строка содержит два
числа: STEP и MOD (1 £ STEP, MOD £ 100000).
Выход. Для каждого теста вывести значение STEP в колонках от 1 до
10, выровненное справа, значение MOD в колонках от 11 до 20, выровненное
справа, и фразу ‘Good Choice‘ или ‘Bad Choice‘, начиная с колонки 25. Если по
входным STEP и MOD будут сгенерированы все числа от 0 до MOD – 1, то выводить
фразу ‘Good Choice‘. Иначе следует выводить фразу ‘Bad Choice‘. После вывода
результата для каждого теста выводить пустую строку.
|
Пример входа |
Пример выхода |
|
3 5 |
3 5
Good Choice |
|
15 20 |
|
|
63923 99999 |
15 20
Bad Choice |
|
|
|
|
63923
99999 Good Choice |
Упражнение 3.2 [Вальядолид, 10683]. Десятичные
часы. Однажды математик Гильберт
Ром изобрел часы с десятичной системой исчисления. День был поделен на 10
часов, в каждом часе было 100 минут, а в каждой минуте – 100 секунд. В задаче
требуется перевести время из традиционной системы в десятичную с точностью до
одной сотой секунды.
Вход. Состоит из нескольких строк. Каждая строка содержит
традиционное время в формате HHMMSSCC, где 0 £ HH £ 23, 0 £ MM £ 59, 0 £ SS £ 59, 0 £ CC £ 99.
Выход. Для каждого теста вывести его соответствующее десятичное
время в формате HMMSSCC, где 0 £ H £ 9, 0 £ MM £ 99, 0 £ SS £ 99, 0 £ CC £ 99.
Значение десятичного времени следует округлить вниз.
|
Пример входа |
Пример выхода |
|
00000000 |
0000000 |
|
23595999 |
9999998 |
|
12000000 |
5000000 |
|
14273467 |
6024846 |
|
02475901 |
1166552 |
4. МАТЕМАТИЧЕСКИЕ
ФУНКЦИИ
Для работы с алгебраическими и
тригонометрическими функциями следует поключить к программе библиотеку <math.h>:
#include <math.h>
Алгебраические функции:
|
Функция |
вызов функции |
|
квадратный корень, |
sqrt(x) |
|
степень числа, xn |
pow(x,n) |
|
экспонента, ex |
exp(x) |
|
натуральный логарифм, ln x |
log(x) |
|
десятичный логарифм, lg x |
log10(x) |
|
модуль целого числа, |x| |
abs(x) |
|
модуль действительного числа, |x| |
fabs(x) |
Тригонометрические функции:
|
функция |
вызов функции |
|
синус, sin(x) |
sin(x) |
|
косинус, cos(x) |
cos(x) |
|
тангенс, tg(x) |
tan(x) |
|
арксинус, arcsin(x) |
asin(X) |
|
арккосинус, arccos(x) |
acos(x) |
|
арктангенс, arctg(x) |
atan(x) |
Константа в библиотеке <math.h> не определена. Ее можно получить,
вычислив arccos(-1):
const double
PI = acos(-1.0);
Функции округления:
|
функция |
вызов функции |
|
округление вверх, |
ceil(x) |
|
округление вниз, |
floor(x) |
При вычислении степеней чисел
иногда удобно воспользоваться соотношением
xn = 
= 
Отсюда, например, следует что
= 
= 
= 
Для вычисления квадратного корня
с удвоенной точностью используют функцию sqrtl.
Упражнение 4.1 [Вальядолид 113]. Сила криптографии. По заданным числам n ³ 1 и p ³ 1 вычислить значение 
,
положительный n - ый корень числа p. Известно, что всегда существует такое целое k, что kn = p.
Вход.
Состоит из последовательности пар чисел n и p, каждое число задается в
отдельной строке. Известно, что 1 £ n £ 200, 1 £ p < 10101, 1 £ k £ 109.
Выход. Для каждой пары чисел n и p вывести значение .
|
Пример входа |
Пример выхода |
2 |
4 |
16 |
3 |
3 |
1234 |
27 |
|
7 |
|
4357186184021382204544 |
|
Упражнение 4.2 [Вальядолид 10509]. Обмануть Мистера Фреймана. Мистер Фрейман – известный
музыкант, учитель и Нобелевский лауреат. Однажды он в уме смог вычислить
значение кубического корня из числа 1729.03 до трех знаков после запятой,
получив 12.002.
Приближенно
вычислить квадратный корень можно следующим образом. Пусть 
= a + dx, где a – целое, 0 £ dx < 1. Тогда n = (a + dx)2 =
a2 + 2 * a * dx + (dx)2. Если значение dx мало, то
при приближенном вычислении слагаемое (dx)2 можно не
учитывать, то есть можно положить что n = a2 + 2 * a
* dx. Здесь dx = (n – a2) / 2a. В
задаче требуется построить аналогичную схему для вычисления приближенного
значения кубического корня.
Вход. Каждая строка содержит
действительное значение n в промежутке от 0 до 1000000 включительно.
Последняя строка содержит 0 и не обрабатывается.
Выход. Для каждого теста вывести приближенное значение 
, округленное до четырех цифр после десятичной точки.
|
Пример входа |
Пример выхода |
1729.0300 |
12.0024 |
|
64.0000 |
4.0000 |
|
63.9990 |
4.3703 |
|
0 |
|
Упражнение 4.3 [Вальядолид 10773]. Назад к математике средней
школы. Необходимо
пересечь реку длиной d метров. Скорость течения реки v м/с,
скорость лодки – u м/с. Существует возможность пересечь реку либо за
минимальное время, либо по кратчайшему пути (пути, перпендикулярному течению
реки). Если существуют такие два разные пути, то вывести неотрицательную
разницу времен P с тремя точками после запятой, за которую их можно преодолеть.
Иначе вывести фразу “can’t determine”.
Вход. Входные данные состоят из
нескольких тестов. Каждый тест в одной строке содержит три числа d, v,
u (v и u – неотрицательны, d – положительно).
Выход. Для каждого теста вывести в отдельной строке его номер как указано в
примере, разницу времен P, если существует два разных пути или фразу “can’t
determine” иначе.
|
Пример входа |
Пример выхода |
|
3 |
Case 1: 1.079 |
|
8 5 6 |
Case 2: 0.114 |
|
1 2 3 |
Case 3: 0.135 |
|
1 5 6 |
|
Упражнение 4.4 [Вальядолид 10784]. Диагональ. Количество диагоналей у выпуклого n - угольника не
менее N. Чему равно минимально возможное значение n?
Вход. Каждая входная стока содержит
положительное целое число N (N £ 1015) – количество
проведенных диагоналей. Значение N = 0 является концом входных данных и не
обрабатывается.
Выход. Для каждого теста вывести его номер и минимально возможное число n
сторон многоугольника.
|
Пример входа |
Пример выхода |
|
10 |
Case 1: 7 |
|
100 |
Case 2: 16 |
|
1000 |
Case 3: 47 |
|
0 |
|
УКАЗАНИЯ К РЕШЕНИЮ
УПРАЖНЕНИЙ
Упражнение 1.1.1. Можно найти замкнутую формулу представленного выражения,
совершив ряд математических преобразований:
* * * … * =
* 
* 
* … * 
Заметим, что
=
= 
= 1
Поэтому искомое выражение равно
*
* * 
= 
* 
= 
Программа, вычисляющая значение
выражения при помощи цикла, имеет вид:
#include <stdio.h>
int i, n = 100;
double
res;
void main(void)
{
res = 1;
for(i = 2; i <= n; i++)
res *= (i * i * i - 1.0) / (i * i * i + 1);
printf("%lf\n", res);
}
Упражнение 1.2.1 [Топкодер, SRM 343, PersistentNumber]. Последовательно вычисляем
значения x, p(x), p(p(x)), … до тех
пор, пока очередное число в последовательности не станет меньше 10. Функция p(x) вычисляет произведение цифр
числа x.
#include <stdio.h>
int p(int
x)
{
return (x
< 10) ? x : p(x / 10) * (x % 10);
}
class PersistentNumber
{
public:
int
getPersistence(int n)
{
return (n
< 10) ? 0 : getPersistence(p(n)) + 1;
}
};
Упражнение
1.2.2 [Топкодер, TCHS 29, ReverseSums].
В цикле для
заданного n
находим число, записанное теми же цифрами, но в обратном порядке. Складываем
его с исходным значением n.
#include <stdio.h>
class ReverseSums
{
public:
int getSum(int n)
{
int m = 0, nn = n;
while(n)
m = m * 10 + n %10,
n /= 10;
return nn +
m;
}
};
Упражнение 1.3.1 [Топкодер, SRM 326, AdditionCycles]. В задаче достаточно
промоделировать описанный процесс преобразования числа. Начиная со входного
значения n, повторяем процесс
преобразования, пока снова не получим это же число. Параллельно подсчитываем
количество таких преобразований в переменной len.
Описанное преобразование над
числом n можно записать и одной
командой:
n
= n%10*10 + (n%10 + n/10)%10
#include <stdio.h>
class
AdditionCycles{
public:
int
cycleLength(int n)
{
int sum, k = -1, len = 0, Initn = n;
while(Initn
!= k)
{
sum = n%10 + n/10;
k = n%10*10 + sum%10;
len++; n = k;
}
return len;
}
};
Программу можно упростить
следующим образом, записав преобразование числа в одной команде:
#include <stdio.h>
class AdditionCycles{
public:
int
cycleLength(int n)
{
int len = 0, Initn = n;
do{
n =
n%10*10 + (n%10 + n/10)%10, len++;
} while(n != Initn);
return len;
}
};
Упражнение 2.1 [Вальядолид, 10633]. На редкость простая
задача. Пусть N
= 10 * X + a, где а – последняя цифра числа N (0 £ a
£ 9). Тогда M = X, N – M =
10 * X + a – X = 9 * X + a. Обозначим n = N – M. Тогда a = n
mod 9, X = (n – a) / 9. Очевидно, что искомым будет N = 10 * X + a = 10 * (n
– a) / 9 + n mod 9.
Если a = n
mod 9 = 0, то последняя цифра a может равняться 9, так как 9 mod 9 = 0.
Тогда X = (n – 9) / 9 = n / 9 – 1, откуда N = 10 * X + a =
10 * (n / 9 + 1) + 9.
Таким образом если значение N – M
делится на 9, то существует два разных значения N. Иначе – одно.
Пример. Если N = 19, то M = 1 и N – M =
18. При N = 20 получим M = 2 и N – M = 18. Если N – M = 18 (делится на 9), то
существует два разных значения N: 19 и 20.
Реализация. Объявим переменные a, n,
x типа double.
double a,n,x;
Вводим n = N – M.
Последовательно вычисляем значения a, x и выводим результат
согласно приведенному выше анализу.
while (scanf("%lf",&n),n
> 0)
{
a = n % 9;
x = (n - a) / 9;
if (!a)
printf("%lf ",10*(x-1)+9);
printf("%lf\n",10*x+a);
}
Упражнение 2.2 [Вальядолид, 10783]. Сумма нечетных чисел. Пересчитаем значения a и b так, чтобы a
равнялось наименьшему нечетному числу из интервала [a, b], а b
– наибольшему. Если a > b, то сумма рана 0. Иначе сумму всех
нечетных чисел из интервала [a, b] считаем по формуле суммы
арифметической прогрессии. Поскольку значения a и b нечетные, то
количество нечетных чисел в интервале [a, b] равно (b - a)
/ 2 + 1, а сумма всех нечетных чисел равна
Пример. Путь a = 4, b = 10. После пересчета интервал [4, 10]
превратится в [5, 9]. Количество нечетных чисел равно (9 – 5) / 2 + 1 = 3.
Сумма всех нечетных чисел равна (5 + 9) / 2 * 3 = 21.
Реализация. После прочтения входных данных
пересчет границ интервала совершаем по правилу: если значение a четно,
то увеличиваем его на 1; если b четно, то уменьшаем его на 1. Далее
используем формулу суммы членов арифметической прогрессии.
scanf("%d", &tests);
for(i = 1; i <= tests; i++)
{
scanf("%d
%d", &a, &b);
if (a % 2 ==
0) a++;
if (b % 2 ==
0) b--;
if (b < a)
res = 0;
else res =
(b + a) * ((b - a) / 2 + 1) / 2;
printf("Case
%d: %d\n", i, res);
}
Упражнение 2.3 [Тимус, 1068]. Сумма. Если считать сумму,
последовательно складывая числа от 1 до n,
то получим Time Limit. Следует воспользоваться формулой суммы арифметической
прогрессии. Если n > 0, то
результатом будет
res = (1 + n) * n / 2
Иначе сумма равна
res = ((1 + n) * (abs(n) + 2)) / 2
Реализация. Читаем входное значение n и вычисляем сумму res согласно приведенным выше формулам.
scanf("%d", &n);
if (n >= 1) res = (1 + n) * n / 2;
else res = ((1 + n) * (abs(n) + 2)) / 2;
Выводим результат res.
printf("%d\n", res);
Упражнение 3.1 [Вальядолид, 408]. Однородный генератор. Положим seed(0) = 0. Если будут сгенерированы
по выше приведенной формуле все числа от 0 до MOD – 1, то seed(i) ¹ 0, i = 1, 2, …, MOD – 1. При этом seed(MOD) = 0. Фразу ‘Bad Choice‘
следует выводить, если существует такое i, 1 £ i £ MOD – 1, что seed(i)
= 0.
Реализация. Читаем входные значения STEP и MOD. Положим seed = 0. Совершим MOD – 1 итераций
генерирования псевдослучайных чисел. Если хотя бы на одном этапе получится seed
= 0, то все числа от 0 до MOD – 1 сгенерированы не будут и следует вывести ‘Bad Choice’. Иначе –
‘Good Choice‘.
while(scanf("%d
%d", &step, &mod) == 2)
{
seed = 0;
for(i = 0; i < mod - 1; i++)
{
seed = (seed + step) % mod;
if (!seed) break;
}
if (i == mod
- 1) printf("%10d%10d Good Choice\n\n", step, mod);
else printf("%10d%10d
Bad Choice\n\n", step, mod);
}
Упражнение 3.2 [Вальядолид, 10683]. Десятичные часы. Вычислим,
сколько миллисекунд в обыкновенной нотации приходится на одну миллисекунду в
десятичной. Для этого следует поделить суммарное число
миллисекунд в сутках в десятичной системе (оно равно 10 * 100 * 100 * 100) на
число миллисекунд в обыкновенной (24 * 60 * 60 * 100). Далее следует
вычислить число миллисекунд во входном традиционном времени, умножить его на полученное выше
соотношение и округлить до целого снизу. Полученное десятичное время следует
выводить с ведущими нулями.
Пример. Соотношение между секундой в
десятичной системе и секундой в обыкновенной системе равно 10 * 100 * 100 * 100
/ 24 * 60 * 60 * 100 = 1.1574074. Для второго теста общее число миллисекунд
равно 23 * 3600 * 100 + 59 * 60 * 100 + 59 * 100 + 99 = 8639999. Умножив его на
выше полученное соотношение, получим 8639999 * 1.1574074 = 9999998,7785926.
Округлив значение до целой части, получим 9999998. Это и есть соответствующее
время в десятичной системе.
Реализация. Объявим необходимые переменные. В переменной TotalMiliSeconds содержится количество
миллисекунд в сутках при стандартной записи времени, в переменной TotalDecSeconds
– при десятичной. Переменная rate содержит их отношение.
int h,m,s,c,MiliSeconds;
int TotalMiliSeconds = 24*3600*100;
int TotalDecSeconds = 10*10000*100;
int Res;
double rate = (double)TotalDecSeconds
/ TotalMiliSeconds;
Читаем количество часов h,
минут m, секунд s и миллисекунд c, вычисляем общее
количество миллисекунд MiliSeconds в текущем времени в стандартной
нотации и умножаем полученное значение на rate. Округляем его, выделяя
целое число, и печатаем в формате с обязательным выводом ведущих нулей (если
таковы имеются). Всего выводится 7 цифр, поэтому формат вывода будет
"%07d".
while (scanf("%2d%2d%2d%2d", &h, &m, &s, &c) == 4)
{
MiliSeconds = h * 3600 * 100 + m * 60 * 100 + s * 100 + c;
Res = int(rate
* MiliSeconds);
printf("%07d\n", Res);
}
Упражнение 4.1 [Вальядолид 113]. Сила криптографии. Известно, что = 
= 
= 
. В соответствии с ограничениями
на числа n, p и k достаточно присвоить этим
переменным тип double и вычислить , что в языке С будет записано
как exp(log(p)/n).
Пример. Рассмотрим
третий тест: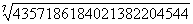 
= 1234.
Реализация. Читаем в цикле (пока не конец файла) значения n и p,
вычисляем и печатаем значение .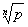
while(scanf("%lf
%lf", &n, &p) == 2)
{
res = exp(log(p) / n);
printf("%.0lf\n", res);
}
Упражнение 4.2 [Вальядолид 10509]. Обмануть Мистера
Фреймана. Если = a + dx,
то n = (a + dx)3 = a3 + 3 * a2
* dx + 3 * a * (dx)2 + (dx)3.
Если отбросить второе и третье слагаемое в правой части, то приближенно имеем
равенство n = a3 + 3 * a2 * dx.
Отсюда dx = (n – a3) / 3a2.
При этом a = 
.
Пример. В первом
тесте n = 1729.03, значит a =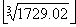 
. = 12. dx = (1729.03 – 123) / (3 * 122)
= (1729.03 – 1728) / 432 = 1.03 / 432 = 0.0001 * 10300 / 432 = 0.0024. Откуда 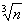= a + dx
= 12 + 0.0024 = 12.0024.
Реализация. Читаем
входное значение n, вычисляем a = =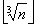 
= 
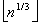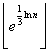. Последнее выражение на языке С запишется как (int)(exp(log(n)/3) + 0.0000001). Перед взятием целой
части следует добавить к exp(log(n)/3)
некое малое значение eps = 0.0000001, чтобы избежать ошибки округления.
Находим значение dx и выводим a + dx с четырьмя знаками
после десятичной точки.
while(scanf("%lf", &n), n > 0)
{
a = (int)(exp(log(n) / 3) + 0.0000001);
dx = (n – a * a * a) / (3 * a * a);
printf("%.4lf\n", a + dx);
}
Упражнение 4.3 [Вальядолид 10773]. Назад к математике средней
школы. Если направить вектор скорости лодки перпендикулярно
течению реки, то достичь второго берега можно за минимальное время. В этом
случае течение реки будет сносить лодку, однако скорость ее приближения к
противоположному берегу будет максимально возможной и равной u м/с.
Время пересечения реки равно d / u. В случае движения по
кратчайшему пути лодку следует направить таким образом, чтобы равнодействующая
ее скорости и скорости течения была направлена перпендикулярна течению реки.
Тогда скорость приближения к берегу равна 
и время пересечения
реки равно d /
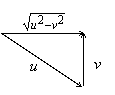
Два пути совпадут, если скорость
реки равна 0, в этом случае необходимо вывести фразу “can’t determine”. Эту
фразу следует также вывести, если скорость течения не меньше скорости лодки (v
³ u). Если скорость лодки равна нулю (u = 0), то неравенство v
³ u справедливо при любом v.
Пример. Рассмотрим входные данные для первого теста. Время пересечения реки за
кратчайшее время равно 8 / 6 = 1.3333. Скорость приближения к берегу в случае
движения по кратчайшему пути равно 
, время преодоления реки – 8 / 
= 2.4121. Разность
вычисленных времен с округлением до трех знаков после запятой равна 1.079.
Реализация. Читаем входные данные и проверяем условия, при которых
не существует двух разных путей. Переменная q
содержит номер текущего теста.
scanf("%lf %lf %lf", &d, &v, &u);
if ((v >= u) || (v == 0.0))
{
printf("Case
%d: can't determine\n", q);
continue;
}
Переменной t1 присваиваем кратчайшее время переправы, переменной t2 – время переправы по кратчайшему
пути. Находим их разность с учетом того, что t2 ³ t1 и печатаем
результат с тремя точками после запятой.
t1 = d / u;
t2 = d / sqrt(u * u – v * v);
res = t2 - t1;
printf("Case
%d: %.3lf\n", q, res);
Упражнение 4.4 [Вальядолид 10784]. Диагональ. Количество диагоналей выпуклого n – угольника
равно n * (n - 3) / 2. Если n * (n - 3) / 2 = N, то
n находим из квадратного уравнения n2 - 3 * n -
2 * N = 0. Положительный корень уравнения равен
Остается округлить сверху
вычисленное значение. Поскольку N £ 1015, то вычисления
следует проводить, используя тип данных long long (__int64)
Пример. Рассмотрим второй тест. Для N =
100 получим
n =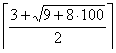 
= 16
Реализация. Читаем входные данные пока N > 0, вычисляем по
формуле результат и выводим его с номером теста.
long long
n,res;
int cs = 1;
while(scanf("%lld", &n), n > 0)
{
res = int(ceil((3
+ sqrtl(9.0 + 8 * n)) / 2));
printf("Case
%d: %lld\n", cs, res);
cs++;
}