ЗАНЯТИЕ
7
1. Наибольший общий делитель. Наименьшее общее кратное. Методы
вычисления, свойства.
2. Расширенный алгоритм Евклида. Описание алгоритма. Примеры.
3. Диофантовы уравнения. Решение уравнения ax + by
= c в целых неотрицательных числах. Теорема о существовании
решения.
4. Обработка строк. Библиотека <string.h>. Длина строки. Конкатенация и
копирование строк. Ввод-вывод строк при помощи функций gets и puts.
5. Задачи.
http://acm.uva.es/problemset:
10104 (Задача Евклида), 10407 (Простое деление), 10548 (Найти правильный
размен), 10673 (Игра с округлением вниз и вверх), 10717 (Монетный завод).
1. НАИБОЛЬШИЙ ОБЩИЙ
ДЕЛИТЕЛЬ. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Определение 1.1. Наибольшим общим делителем (далее НОД) двух
целых чисел a и b, одновременно не равных нулю, называется такое
наибольшее целое число d, на которое a и b делятся без
остатка. Этот факт обозначается так: d = НОД(a, b). Если
оба числа равны нулю, то положим НОД(0, 0) = 0.
Исходя из определения,
имеют место следующие равенства:
НОД(a, b) = НОД(b, a),
НОД(a, b) = НОД(-a, b)
НОД(a, 0) = |a|
Определение 1.2. Наименьшим общим кратным (далее НОК) двух
целых чисел a и b называется наименьшее общее положительное целое
число, кратное как a так и b.
Основная теорема
арифметики утверждает, что любое натуральное число можно представить в виде
произведения простых чисел:
n = ![]() =
= ![]()
Из канонического
разложения следует, что
НОД(a, b) = ![]()
НОК(a, b) = ![]()
Пример 1.1. Рассмотрим числа a = 24, b = 18.
Разложим их на простые множители: 24 = 23 * 3, 18 = 2 * 32.
Следовательно
НОД(24, 18) = 2min(3,1) * 3min(1,2)
= 21 * 31 = 6,
НОК(24, 18) = 2max(3,1) * 3max(1,2)
= 23 * 32 = 8 * 9 = 72
Если НОД(a, b)
= d, то a и b делятся на d. Следовательно их
разница a – b также делится на d. Имеет место следующее
рекурсивное соотношение для вычисления НОД, известное как алгоритм Евклида:
НОД(a, b) = 
Пример 1.2. Пусть a = 32, b = 12. Тогда
НОД(32, 12) = НОД(32 – 12, 12) = НОД(20, 12) =
НОД(20 – 12, 12) = НОД(8, 12) =
НОД(8, 12 – 8) = НОД(8, 4) = НОД(8 – 4, 4) =
НОД(4, 4) = НОД(4 – 4, 4) = НОД(0, 4) = 4
Приведенный метод
вычисления не является оптимальным. Например, для нахождения НОД(100, 2)
следует выполнить 50 операций вычитания. Для ускорения вычисления НОД операцию
вычитания следует заменить операцией взятия остатка от деления:
НОД(a, b) = 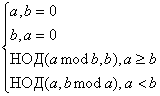
Пример 1.3. Пусть a = 78, b = 14. Тогда
НОД(78, 14) = НОД(78 mod 14, 14) = НОД(8, 14) =
НОД(8, 14 mod 8) = НОД(8, 6) =
НОД(8 mod 6, 6) = НОД(2, 6) = НОД(2, 6 mod 2) =
НОД(2, 0) = 2
Упростим приведенную выше
рекуррентность:
НОД(a, b) = ![]()
Если a < b,
то НОД(a, b) = НОД(b, a mod b) = НОД(b,
a), то есть аргументы функции переставляются. Далее при рекурсивных
вызовах первый аргумент всегда больше второго. Нулем может стать только второй
аргумент b.
Используя тернарный
оператор, функцию gcd (Greater Common Divisor) вычисления НОД можно записать в виде:
int gcd(int a, int b)
{
return (!b) ? a : gcd(b,a % b);
}
Пример 1.4. Пусть a = 14, b = 78. Тогда
НОД(14, 78) = НОД(78, 14) = НОД(14, 8) = НОД(8, 6)
= НОД(6, 2) = НОД(2, 0) = 2
Бинарный алгоритм вычисления НОД имеет вид:
НОД(2*a, 2*b) = 2*НОД(a, b),
если a и b четно
НОД(2*a, b) = НОД(a, b),
если a четно, b нечетно
НОД(a, 2*b) = НОД(a, b),
если a нечетно, b четно
НОД(a, b) = НОД(a – b,
b), если a нечетно, b нечетно, a > b
НОД(a, b) = НОД(a, b
– a), если a нечетно, b нечетно, a £ b
Теорема
1.1. Между НОД и НОК двух чисел
имеет место соотношение:
a * b = НОД(a, b) * НОК(a, b)
Функция lcm (Lowest
Common Multiple) вычисления НОК
имеет вид:
int lcm(int a, int b)
{
return a * b /
gcd(a,b);
}
Заметим, что при
вычислении выражения a * b / gcd(a, b) может возникнуть
переполнение, а при a / gcd(a, b)
* b нет. Здесь подразумевается, что
значения a, b и lcm(a, b) лежат в границах типа int.
Упражнение 1.1. [Вальядолид, 10407]. Простое деление. При делении числа n на d получается
частное q и остаток r. При этом q – максимально возможное
целое, для которого qd £ n, а r = n
– qd. Для любого множества целых чисел {a1, …, ak}
всегда существует такое d, что числа ai mod d
равны.
Вход. Каждая строка является отдельным
тестом и содержит последовательность чисел a1, …, ak,
заканчивающуюся нулем. Последний ноль не принадлежит самой последовательности.
Последовательность содержит не менее 2 и не более 1000 чисел. Не все числа в
последовательности равны между собой. Признаком конца входных данных является
строка с одним нулем.
Выход. Для каждой входной последовательности a1,
…, ak найти максимальное d, для которого при делении ai
на d будут получаться равные остатки.
|
Пример входа |
Пример выхода |
|
701 1059
1417 2312 0 |
179 |
|
14 23 17 32
122 0 |
3 |
|
14 -22 17
-31 -124 0 |
3 |
|
0 |
|
Упражнение 1.2. [Вальядолид, 10717]. Монетный завод. Канадский королевский завод производит
столы, ножки которых составляют из куп монет. Каждый стол имеет четыре ножки, а
каждая ножка должна состоять из разных типов монет. Например, одна ножка может
состоять из четвертушек, другая – из десяток, третья – из одноцентовых, а
четвертая – из двухцентовых монет. Имеется конечное количество типов монет.
Количество монет каждого типа неограниченно. Известна толщина каждого типа
монет. Необходимо определить максимально возможную высоту стола, не большую
заданной величины и минимально возможную высоту стола, не меньшую заданной
величины.
Вход. Состоит из нескольких тестов. Первая строка каждого теста
содержит количество доступных номиналов монет n (4 £ n £ 50) и количество столов T (1 £ T £ 10), которое следует сделать.
Следующие n строк характеризуют толщину монет. Далее идут T строк,
описывающих желаемые высоты столов, которые следует сконструировать. Последний
тест содержит n = T = 0 и не обрабатывается.
Выход. Для каждого теста вывести максимально возможную высоту
стола, не большую желаемой и минимально возможную высоту стола, не меньшую
желаемой.
|
Пример входа |
Пример выхода |
|
4 2 |
800 1200 |
|
50 |
2000 2000 |
|
100 |
|
|
200 |
|
|
400 |
|
|
1000 |
|
|
2000 |
|
|
0 0 |
|
2. РАСШИРЕННЫЙ АЛГОРИТМ ЕВКЛИДА
Алгоритм Евклида можно
расширить для нахождения по заданным a
и b таких целых x и y,
что ax + by = d, где d – наибольший общий делитель a
и b.
Пусть для положительных целых чисел a и b (a
> b) известны g = НСД(b, a mod b), а
также числа x’ и y’, для которых
g = x’
* b + y’ * (a mod b)
Поскольку
a mod b = a – ![]() * b, то
* b, то
g = x’
* b + y’ * (a – ![]() * b) = y’
* a + (x’ – y’ *
* b) = y’
* a + (x’ – y’ * ![]() ) * b = x * a + y * b,
) * b = x * a + y * b,
где
обозначено x = y’, y = x’ – y’ * ![]() .
.
Пусть gcdext(int a,
int b, int *d, int *x, int *y) – функция, которая по входным числам a
и b находит d = НСД(a, b) и такие x, y
что d = a * x + b * y. Для поиска
неизвестных x и y необходимо рекурсивно запустить функцию gcdext(b, a
mod b, d, x, y) и пересчитать значения x и y
по выше приведенной формуле. Рекурсия заканчивается, когда b = 0. При b
= 0 НОД(a, 0) = a и a = a * 1 + 0 * 0, поэтому
полагаем x = 1, y = 0.
Пример 2.1. Найдем решение уравнения 5x + 3y = 1. Вычисление
НОД(5, 3) и нахождение соответствующих x, y произведем в таблице:
|
a |
b |
x |
y |
|
5 |
3 |
-1 |
2 |
|
3 |
2 |
1 |
-1 |
|
2 |
1 |
0 |
1 |
|
1 |
0 |
1 |
0 |
Из таблицы находим, что НОД(5, 3)
= 5 * (-1) + 3 * 2 = 1, то есть x =
-1, y = 2.
Упражнение 2.1. [Вальядолид, 10104]. Задача Евклида. Со времен Евклида известно, что
для любых положительных a и b существуют такие целые x и y,
что ax + by = d, где d – наибольший общий делитель a
и b. По заданным a и b найти x, y, d.
Вход. Каждая строка содержит два числа
a и b, разделенных пробелом (a, b £ 109).
Выход. Для каждого теста вывести три
числа x, y, d, разделенных пробелом. Если существует
несколько пар x и y, то вывести ту пару, для которой x £ y и выражение |x| + |y| минимально.
|
Пример входа |
Пример выхода |
|
4 6 |
-1 1 2 |
|
17 17 |
0 1 17 |
|
5 3 |
-1 2 1 |
Упражнение 2.2. [Вальядолид, 10673] Игра с
округлением вниз и вверх.
Теорема. Для двух целых чисел x и k всегда существуют
такие целые p и q, что
x = p![]() + q
+ q![]()
По заданным x и k
необходимо найти хотя бы одну такую пару p и q.
Вход. Первая строка содержит
количество тестов t (1 £ t £ 1000). Каждая следующая строка содержит два положительных целых числа x
и k (x, k < 108).
Выход. Для каждого теста вывести в отдельной строке два числа: p
и q. Если таких пар существует несколько, то вывести одну из них.
Значения p![]() и q
и q![]() помещаются в 64-битовый целый тип.
помещаются в 64-битовый целый тип.
|
Пример входа |
Пример выхода |
|
3 |
1 1 |
|
5 2 |
1 1 |
|
40 2 |
0 6 |
|
2444 6 |
|
3. ДИОФАНТОВЫ УРАВНЕНИЯ
Диофантовыми
уравнениями называются уравнения вида
P(x1, x2, ..., xn)
= 0,
где P(x1, ..., xn) – многочлен
с целыми коэффициентами.
В этой главе рассмотрим алгоритм
нахождения решения линейного диофантового уравнения с двумя неизвестными: a*x
+ b*y = c.
Теорема 3.1. Уравнение
a*x + b*y = c имеет решения в целых числах тогда и только тогда, когда c делится на НОД(a, b).
Теорема 3.2. Если пара (x0, y0) является решением уравнения ax + by = c, то все множество его решений (x, y) описывается формулой:
x = x0 + kb,
y = y0 – ka,
где
k Î Z. При этом a(x
+ kb) + b(y – ka) = c.
Для нахождения хотя бы одного
решения (x0, y0) уравнения ax
+ by = c следует найти решение (x’, y’) уравнения ax + by = d (d – наибольший общий делитель
чисел a и b) при помощи расширенного алгоритма Евклида, после чего
умножить полученное решение на k = c / d. То есть
x0 = x’
* c / d,
y0 = y’ * c / d
Пример 3.1. Найти множество решений уравнения 5*x + 3*y = 7.
1. Уравнение имеет решения, так
как d
= НОД(5, 3) = 1, 7
делится на 1.
2. Находим решение уравнения 5*x’
+ 3*y’ = 1 при помощи расширенного
алгоритма Евклида (пример 1.2.1): (x’, y’) = (-1, 2).
3. Находим решение (x0, y0) исходного диофантового уравнения:
x0 = -1 * 7 / 1 = -7,
y0 = 2 * 7 / 1 = 14
Согласно теореме 1.3.2. множество
решений диофантового уравнения имеет вид:
(x,
y) = (-7 + 3*k, 14 – 5*k)
Упражнение 3.1. [Вальядолид, 10548]. Найти правильный размен.
В древние
времена люди вместо денег обменивались товарами. В наличии имеются два типа
товаров: A и B. Покупатель желает приобрести товар на сумму c > 0.
Стоимости товаров A и B соответственно равны a и b. Если одно из
значений a или b отрицательно, то продавец может этим товаром
давать сдачу. Одновременно отрицательными a и b быть не могут.
Сколькими способами покупатель может приобрести товар на сумму c, если
это возможно?
Вход. Первая строка содержит
количество тестов n (0 < n < 1001). Каждая следующая строка
содержит три числа a, b и c (0 < |a|, |b|,
|c| < 231).
Выход. Для каждого теста вывести количество комбинаций, которыми
покупатель может приобрести товар ровно
на сумму c. Если приобрести товар невозможно, то вывести
сообщение “Impossible”. Если число комбинаций бесконечно, то вывести
“Infinitely many solutions”.
|
Пример входа |
Пример выхода |
|
3 |
3 |
|
2 3 15 |
Infinitely
many solutions |
|
2 –3 5 |
Impossible |
|
10 36 7 |
|
4. ОБРАБОТКА СТРОК
В этом разделе мы не будем
касаться класса string, а рассмотрим, как обрабатывались строки на языке Си до
появления стандартной библиотеки шаблонов.
Строки представляются в памяти
компьютера как массив элементов char. Первый символ строки доступен как нулевой
элемент массива, второй символ – как первый и так далее. В конце строки всегда
стоит символ ‘\0’ (нуль-символ). То есть строки в Си завершаются нулем. Такой
подход позволяет снять ограничения с длины строк. Строка может быть такой
длины, какой позволяет память для ее хранения. Символ ‘\0’ не видим в строковом
выражении, но он добавляется как последний элемент при запоминании строки. Так,
строка “ABC” содержит 4 символа, а не три.
Пример 4.1. Объявим две строки s
и t. Строку t проинициализируем данными.
char s[10],t[10] = "This";
Для вывода строк при помощи
функции printf пользуются форматом “%s”:
printf("%s\n",t);
Вывести строку можно и при помощи
цикла посимвольно:
for(i=0;t[i];i++) printf("%c",t[i]);
printf("\n");
Цикл продолжается до тех пор,
пока очередной выводимый символ не будет иметь ASCII код, равный 0.
Для работы со строками существует
набор функций, объявленный в библиотеке <string.h>. Рассмотрим некоторые из них.
|
функция |
описание функции |
|
size_t strlen(const
char *string) |
длина строки |
|
|
Копирует строку |
|
|
Конкатенация строк |
Пример 4.2. Объявим строку s и
найдем ее длину.
char s[] = "This";
printf("Length of %s is %d\n",s,strlen(s));
Пример 4.3. Создадим строку t,
состоящую из 10 копий “abc”.
char s[] = "abc";
char t[31];
for(i=0;i<10;i++) strcat(t,s);
printf("%s\n",t);
Следующие функции позволяют
читать и выводить строки из и на консоль.
|
функция |
описание функции |
|
|
чтение строки в символьный массив |
|
|
вывод строки на консоль |
Пример 4.4. Прочитать текст и вывести его на консоль. Длина каждой
строки не более 100.
char s[100];
while(gets(s)) puts(s);
УКАЗАНИЯ К РЕШЕНИЮ УПРАЖНЕНИЙ
Упражнение 1.1. [Вальядолид, 10407]. Простое деление. Из условия задачи следует, что
a1 = d * r1
+ rest
a2 = d * r2
+ rest
…
ak = d * rk
+ rest
Поскольку d максимально ,
то НОД(r1, r2, …, rn) =
1. Далее имеем:
a2 – a1 = d
* (r2 – r1)
a3 – a2 = d
* (r3 – r2)
…
ak – ak-1
= d * (rk – rk-1)
Откуда d = НОД(|a2
– a1|, |a3 – a2|, …, |ak
– ak-1|).
Реализация. Основной цикл программы состоит
в чтении последовательности чисел {a1, …, ak}
и последовательном вычислении значения НОД(|a2 – a1|,
|a3 – a2|, …, |ak – ak-1|).
#include <stdio.h>
#include <math.h>
int a,b,res;
int gcd(int a, int b)
{
return (!b) ? a : gcd(b, a % b);
}
void main(void)
{
while(scanf("%d
%d",&a,&b),a)
{
res = abs(a-b); a = b;
while(scanf("%d",&b),b)
{
res = gcd(res,abs(a-b));
a = b;
}
printf("%d\n",res);
}
}
Упражнение 1.2. [Вальядолид, 10717]. Монетный завод. Если a, b, c, d –
толщины четырех типов монет, то минимально возможная высота стола, который
можно сделать, равна h = НОК(a, b, c, d).
Обозначим через low максимально возможную высоту стола, не большую
желаемой величины Height. Тогда low должно делиться на h и
быть максимально возможным значением, не большим Height. Отсюда
low = ![]() * h
* h
Если вычисленное low равно
Height (что возможно в случае когда Height делится на h
без остатка), то минимально возможная высота стола more, не меньшая Height,
также равна Height. Иначе она равна low + h.
Остается перебрать все возможные
четверки толщин номиналов монет и вычислить максимум среди всевозможных low
и минимум среди всевозможных more.
Пример. Рассмотрим набор монет из первого теста, желаемая
высота стола равна 1000. Имея 4 монеты с толщинами 50, 100, 200, 400 можно
конструировать столы, высоты которых кратны НОК(50, 100, 200, 400) = 400.
Искомые высоты столов, которые можно сделать, соответственно равны 800 и 1200.
Реализация. Входные тесты подобраны так, что
при решении задачи следует работать с типом unsigned (32 - битовое целое,
положительное). Объявим все переменные типа unsigned.
#include <stdio.h>
unsigned gcd(unsigned
a,unsigned b)
{
return !a ? b : gcd(b%a,a);
}
void main(void)
{
unsigned i,n,t,g;
unsigned x1,x2,x3,x4;
unsigned low,Less,Greater,Height;
unsigned coins[50];
while(scanf("%d
%d",&n,&t),n+t>0)
{
for(i=0;i<n;i++)
scanf("%d",&coins[i]);
Для каждой прочитанной желаемой
высоты стола Height проводим выше описанный алгоритм. Обозначим через Less
максимум среди всевозможных low, а через Greater – минимум среди всевозможных more.
Проинициализируем их.
while(t--)
{
scanf("%d",&Height);
Greater = 0xFFFFFFFF;
Less = 0;
Перебираем все возможные четверки
номиналов монет x1 < x2< x3 < x4 (номиналы
монет хранятся соответственно в coins[x1], coins[x2], coins[x3],
coins[x4]).
for(x1=0;x1<n-3;x1++)
for(x2=x1+1;x2<n-2;x2++)
for(x3=x2+1;x3<n-1;x3++)
for(x4=x3+1;x4<n;x4++)
{
Вычисляем НОК толщин монет g =
НОК(coins[x1], coins[x2], coins[x3], coins[x4]).
g = coins[x1] * coins[x2] / gcd(coins[x1],coins[x2]);
g = g * coins[x3] / gcd(g,coins[x3]);
g = g * coins[x4] / gcd(g,coins[x4]);
Для каждой четверки номиналов
пересчитываем значения Less и Greater.
low = Height / g * g;
if (low > Less) Less = low;
if (low != Height)
low += g;
if (low < Greater) Greater = low;
}
printf("%u %u\n",Less,Greater);
}
}
}
Упражнение 2.1. [Вальядолид, 10104]. Задача Евклида. Описание алгоритма приведено в разделе
2.
Реализация. Для решения задачи достаточно
прочитать входные данные, вызвать функцию gcdext и напечатать результат.
#include <stdio.h>
int a,b,d,x,y;
void gcdext(int a,int b,
int *d, int *x, int *y)
{
int s;
if (b == 0)
{
*d = a; *x = 1; *y = 0;
return;
}
gcdext(b,a % b,d,x,y);
s = *y;
*y = *x - (a / b) * (*y);
*x = s;
}
void main(void)
{
while(scanf("%d %d",&a,&b)
== 2)
{
gcdext(a,b,&d,&x,&y);
printf("%d %d %d\n",x,y,d);
}
}
Упражнение 2.2. [Вальядолид, 10673]. Игра с округлением вниз
и вверх. Если x
нацело делится на k, то ![]() =
= ![]() = x / k.
Выбрав p = 0, q = k, получим: 0 * (x / k) + k
* (x / k) = x. Пусть x не делится на k. Если
n =
= x / k.
Выбрав p = 0, q = k, получим: 0 * (x / k) + k
* (x / k) = x. Пусть x не делится на k. Если
n = ![]() , то m =
, то m = ![]() = n + 1.
Поскольку НОД(n , m) = НОД(n , n + 1) = 1, то
исходя из расширенного алгоритма Евклида, существуют такие целые t и u,
что 1 = tn + um. Помножив равенство на x, получим x
= xtn + xum, откуда p = xt, q = xu.
= n + 1.
Поскольку НОД(n , m) = НОД(n , n + 1) = 1, то
исходя из расширенного алгоритма Евклида, существуют такие целые t и u,
что 1 = tn + um. Помножив равенство на x, получим x
= xtn + xum, откуда p = xt, q = xu.
Пример. Для первого теста имеет место соотношение: 5 = 1 * 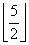 + 1 *
+ 1 * 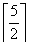 = 1*2 + 1*3.
= 1*2 + 1*3.
Реализация. При вычислении используем
64-битовый целый тип long long. Функция gcdext выглядет так же, как и в задаче
Вальядолид, 10548.
#include <stdio.h>
#include <math.h>
typedef long long i64;
i64 tests,x,k,g,t,u;
i64 n,m,p,q;
void gcdext(i64 a,i64 b,
i64 *d, i64 *x, i64 *y) { ... }
void main(void)
{
scanf("%d",&tests);
while(tests--)
{
scanf("%lld
%lld",&x,&k);
Если k = 0, то
устанавливаем p = 0, q = k.
if (x % k == 0) { p
= 0; q = k;}
else
{
Иначе вычисляем n = ![]() и m =
и m = ![]() , запуская расширенный алгоритм Евклида. Он находит такие t
и u, что 1 = tn + um. Далее находим p = xt, q
= xu и выводим результат.
, запуская расширенный алгоритм Евклида. Он находит такие t
и u, что 1 = tn + um. Далее находим p = xt, q
= xu и выводим результат.
n =
(int)floor(1.0*x/k); m = (int)ceil(1.0*x/k);
gcdext(n,m,&g,&t,&u);
p = t*x; q = u*x;
}
printf("%lld
%lld\n",p,q);
}
}
Упражнение 3.1. [Вальядолид,
10548]. Найти правильный размен. Если покупатель получит x штук товара A и y
штук товара B, заплатив при этом сумму c, то получим уравнение ax
+ by = c. Уравнение имеет решения тогда и только тогда, когда c
делится на НОД(a, b).
Если
одно из значений a или b отрицательно, то уравнение ax + by
= c имеет бесконечно много решений. Действительно, если (x0,
y0) – решение, то пара (x0 + kb, y0
– ka) будет также решением для любого целого отрицательного k,
для которого y0 – ka ³ 0 (если b < 0) или для
любого натурального k, для которого x0 + kb ³ 0 (если a
< 0).
Если решение существует и оба
значения a и b положительны, сокращаем a, b, c
на их общий делитель и при помощи расширенного алгоритма Евклида находим x’,
y’, для которых ax’ + by’ = 1. Помножив последнее
равенство на c и положив x0 = cx’ и y0
= cy’, получим пару (x0, y0),
являющуюся решением уравнения ax + by = c.
Из теоремы 1.3.2. следует, что
все решения уравнения имеют вид (x0 + kb, y0
– ka), где k – целое число. Поскольку в задаче решения должны
быть неотрицательными, то имеют место следующие неравенства: x0
+ kb ³ 0, y0 – ka
³ 0. Откуда имеем следующие ограничения: k ³ ![]() , k £
, k £ ![]() . Количество решений
уравнения ax + by = c, для которых x ³ 0, y
³ 0, равно
. Количество решений
уравнения ax + by = c, для которых x ³ 0, y
³ 0, равно ![]() –
– ![]() + 1.
+ 1.
Пример. Рассмотрим первый тест, где следует найти количество решений уравнения 2x
+ 3y = 15 в целых числах. Числа 2 и 3 взаимно простые, находим x’и
y’, для которых 2x’ + 3y’ = 1. Из расширенного алгоритма
Евклида имеем: x’ = -1, y’ = 1. Помножив их на 17, получим x0
= 17x’ = -17, y0 = 17y’ = 17. Имея одно
решение (x0, y0) = (-17, 17), можно описать
множество всех решений исходного уравнения согласно выше приведенной лемме: x
= -17 + 3k, y = 17 – 2k. Оба значения должны быть
неотрицательными, следовательно -17 + 3k ³ 0, y = 17 – 2k ³ 0. Или то же самое что 3k
³ 17, 17 ³ 2k. Откуда k ³![]() = 6, k £
= 6, k £ ![]() = 8. Объединяя
ограничения на k, получим: 6 £ k £ 8. То есть
существует 3 варианта размена.
= 8. Объединяя
ограничения на k, получим: 6 £ k £ 8. То есть
существует 3 варианта размена.
Для второго теста имеем уравнение
2x – 3y = 5. Одним из его решений будет x0 = 1,
y0 = -1. Все множество решений описывается формулой: x
= 1 – 3k, y = -1 – 2k. Для всех отрицательных k
значения x и y будут положительными, и удовлетворять условию
задачи.
Для третьего теста решений не
существует, так как для любых натуральных x и y значение 10x
+ 36y всегда четно и не может равняться 7.
Реализация. При вычислении используем
64-битовый целый тип long long. Для простоты использования переопределим тип
long long на i64.
#include <stdio.h>
#include <math.h>
typedef long long i64;
i64 i,n,a,b,c;
i64 temp,d,x,y;
i64 kmin, kmax, res;
i64 gcd(i64 a, i64 b)
{
return (!a) ? b : gcd(b % a, a);
}
void gcdext(i64 a,i64 b,
i64 *d, i64 *x, i64 *y)
{
i64 s;
if (b == 0)
{
*d = a; *x = 1; *y = 0;
return;
}
gcdext(b,a % b,d,x,y);
s = *y;
*y = *x - (a / b) * (*y);
*x = s;
}
void main(void)
{
scanf("%lld",&n);
for(i=0;i<n;i++)
{
scanf("%lld %lld
%lld",&a,&b,&c);
Вычисляем наибольший общий
делитель d чисел a и b. Если c не делится на d,
то выводим сообщении о невозможности произведения размена.
d = gcd(a,b);
if (c % d > 0)
{
printf("Impossible\n");
continue;
}
Если a или b
отрицательно, то существует бесконечно много вариантов произведения размена.
if ((a < 0) || (b < 0))
{
printf("Infinitely many
solutions\n"); continue;
}
Сокращаем входные значения a,
b, c на их общий делитель d. Запускаем процедуру
расширенного алгоритма Евклида и находим пару (x, y) – решение
уравнения ax + by = c.
a /= d; b /= d; c /= d;
gcdext(a,b,&d,&x,&y);
x *= c; y *= c;
Ищем нижнюю kmin и верхнюю
kmax границы для переменной k, откуда и получаем количество
решений уравнения ax + by = c. Поскольку a, b,
x, y – целые, то чтобы не потерять точность вычислений, помножим
дроби –x / b и y / a на действительное число 1.0.
kmin = (i64)ceil(-1.0*x / b); kmax =
(i64)floor(1.0*y / a);
res = (i64)kmax - kmin + 1;
Если значение res не равно
нулю, то выводим его. Иначе печатаем сообщение о том, что произвести размен
невозможно.
if (res) printf("%lld\n",res);
else printf("Impossible\n");
}
}